题目内容
设数列{xn}满足x1＞0，xn+1=
，n=1，2，3…那么（ ）
| 3(1+xn) |
| 3+xn |
| A、数列{xn}是单调递增数列 |
| B、数列{xn}是单调递减数列 |
| C、数列{xn}或是单调递增数列，或是单调递减数列 |
| D、数列{xn}既非单调递增数列，也非单调递减数列 |
考点：数列的函数特性
专题：等差数列与等比数列
分析：数列{xn}满足x1＞0，xn+1=
，可得xn＞0，?n∈N*．再计算xn+1-xn与0比较即可得出．
| 3(1+xn) |
| 3+xn |
解答：
解：∵数列{xn}满足x1＞0，xn+1=
，可得xn＞0，?n∈N*．
∴xn+1-xn=
=
，
∴与所给出的x1有关，数列{xn}既非单调递增数列，也非单调递减数列．
故选：D．
| 3(1+xn) |
| 3+xn |
∴xn+1-xn=
3+3xn-3xn-
| ||
| 3+xn |
3-
| ||
| 3+xn |
∴与所给出的x1有关，数列{xn}既非单调递增数列，也非单调递减数列．
故选：D．
点评：本题考查了数列的单调性、“作差法”，属于基础题．
练习册系列答案
相关题目
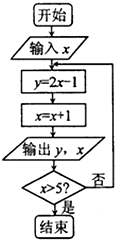如程序框图所示已知集合A={x|框图中输出的x值}，集合B={y|框图中输出的y值}，当x=1时A∩B=（ ）| A、∅ | B、{3} |
| C、{1，3，5} | D、{3，5} |