题目内容
17.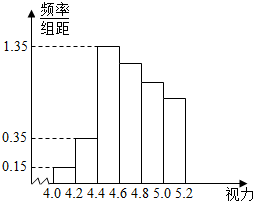 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为X,求X的分布列和数学期望.
附:
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
分析 (1)设各组的频率为fi(i=1,2,3,4,5,6),由已知得后四组频数依次为27,24,21,18,由此能求出估计全年级视力在5.0以下的人数.
(2)求出K2,由此能求出在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系.
(Ⅲ)依题意9人中年级名次在1~50名和951~1000名分别有3人和6人,X可取0、1、2、3,分别求出相应在的概率,由此能求出X的分布列和X的数学期望.
解答 解:(1)设各组的频率为fi(i=1,2,3,4,5,6),
由图可知,第一组有3人,第二组7人,第三组27人,…(1分)
因为后四组的频数成等差数列,
所以后四组频数依次为27,24,21,18…(2分)
所以视力在5.0以下的频率为:$\frac{3+7+27+24+21}{100}$=0.82,
故全年级视力在5.0以下的人数约为$1000×\frac{82}{100}=820$…(3分)
(2)${k^2}=\frac{{100×{{(41×18-32×9)}^2}}}{50×50×73×27}=\frac{300}{73}≈4.110>3.841$
因此在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系.…(6分)
(Ⅲ)依题意9人中年级名次在1~50名和951~1000名分别有3人和6人,X可取0、1、2、3,…(7分)
$P(X=0)=\frac{C_6^3}{C_9^3}=\frac{20}{84}$,
$P(X=1)=\frac{C_6^2C_3^1}{C_9^3}=\frac{45}{84}$,
$P(X=2)=\frac{C_6^1C_3^2}{C_9^3}=\frac{18}{84}$,
$P(X=3)=\frac{C_3^3}{C_9^3}=\frac{1}{84}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{20}{84}$ | $\frac{45}{84}$ | $\frac{18}{84}$ | $\frac{1}{84}$ |
X的数学期望$E(X)=0×\frac{20}{84}+1×\frac{45}{84}+2×\frac{18}{84}+3×\frac{1}{84}=1$…(12分)
点评 本题考查频率分布直方图的应用,考查离散型机随机变量概率分布列、数学期望的求法,是中档题,解题时要认真审题,注意排列组合的合理运用.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案 某校举行一次安全知识教育检查活动,从全校1500名学生中随机抽取50名参加笔试,测试成绩的频率分布表如下:
某校举行一次安全知识教育检查活动,从全校1500名学生中随机抽取50名参加笔试,测试成绩的频率分布表如下:| 分组(分数段) | 频数(人数) | 频率 |
| [50,60) | a | 0.08 |
| [60,70) | 13 | 0.26 |
| [70,80) | 16 | 0.32 |
| [80,90) | 10 | 0.20 |
| [90,100) | b | c |
| 合计 | 50 | 1.00 |
(Ⅱ)根据(Ⅰ)得到的频率分布直方图估计全校学生成绩的中位数,选择这种数字特征来描述该校学生对安全知识的掌握程度的缺点是什么?
| A. | v(t)=-4t+8 | B. | v(t)=4t-8 | C. | v(t)=-8t+2 | D. | v(t)=8t-2 |
| A. | 32 | B. | 80 | C. | -16或32 | D. | -64或80 |
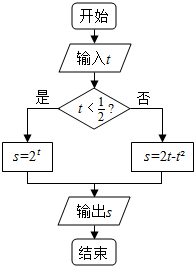
| A. | [0,1] | B. | [$\frac{3}{4}$,$\sqrt{2}$] | C. | [0,$\sqrt{2}$] | D. | [1,$\sqrt{2}$) |
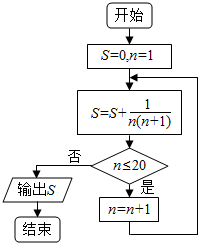
| A. | $\frac{19}{20}$ | B. | $\frac{20}{21}$ | C. | $\frac{21}{22}$ | D. | $\frac{22}{23}$ |
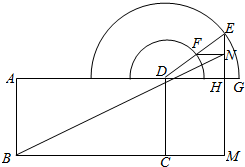 如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.
如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.