题目内容
9.执行如图所示的程序框图,如果输入的t∈[-1,2],则输出的s属于( )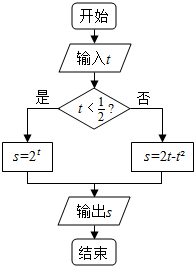
| A. | [0,1] | B. | [$\frac{3}{4}$,$\sqrt{2}$] | C. | [0,$\sqrt{2}$] | D. | [1,$\sqrt{2}$) |
分析 该程序的作用是计算一个分段函数的函数值,由条件为t<$\frac{1}{2}$我们可得,分段函数的分类标准,由分支结构中是否两条分支上对应的语句行,我们易得函数的解析式,从而确定S的区间.
解答 解:执行程序框图,有
输入的t∈[-1,2],
S=$\left\{\begin{array}{l}{{2}^{t}}&{t<\frac{1}{2}}\\{2t-{t}^{2}}&{t≥\frac{1}{2}}\end{array}\right.$,
输出S的值,
由-1$≤t<\frac{1}{2}$时,S=2t∈[$\frac{1}{2}$,$\sqrt{2}$);
$\frac{1}{2}≤t≤2$时,S=2t-t2=1-(t-1)2∈[0,1],
此分段函数在t∈[-1,2]时,输出的s属于[0,$\sqrt{2}$).
故选:D.
点评 本题主要考察程序框图及数形结合能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.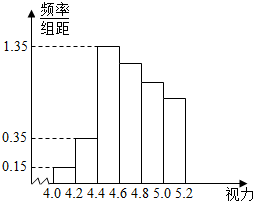 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,
能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为X,求X的分布列和数学期望.
附:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为X,求X的分布列和数学期望.
附:
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
4.下列函数中,同时满足条件①f(-x)=-f(x);②若x1<x2有f(x1)<f(x2)的为( )
| A. | y=x+1 | B. | y=2cosx | C. | y=-$\frac{1}{x}$ | D. | y=x|x| |
14.在框图中,设x=2,并在输入框中输入n=4;ai=i(i=0,1,2,3,4).则此程序执行后输出的S值为( )


| A. | 26 | B. | 49 | C. | 52 | D. | 98 |
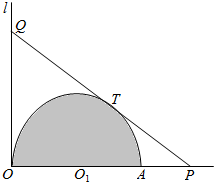 如图,阴影部分为古建筑物保护群所在地,其形状是以O1为圆心,半径为1km的半圆面.公路l经过点O,且与直径OA垂直,现计划修建一条与半圆相切的公路PQ(点P在直径OA的延长线上,点Q在公路l上),T为切点.
如图,阴影部分为古建筑物保护群所在地,其形状是以O1为圆心,半径为1km的半圆面.公路l经过点O,且与直径OA垂直,现计划修建一条与半圆相切的公路PQ(点P在直径OA的延长线上,点Q在公路l上),T为切点.