题目内容
20.已知直线l:kx-y+k-$\sqrt{3}$=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,若|AB|=4$\sqrt{3}$,则|CD|=8$\sqrt{3}$.分析 根据直线与圆相交,圆x2+y2=(2$\sqrt{3}$)2可知:圆心为(0,0),半径r=2$\sqrt{3}$,弦长为|AB|=4$\sqrt{3}$=2r,说明直线过圆心.求解k的值.得到直线AB的倾斜角,根据AOC和OBD是两个全等的直角三角形,OA=OB=2$\sqrt{3}$,即可求出OC和OD.即可得到|CD|的长度.
解答 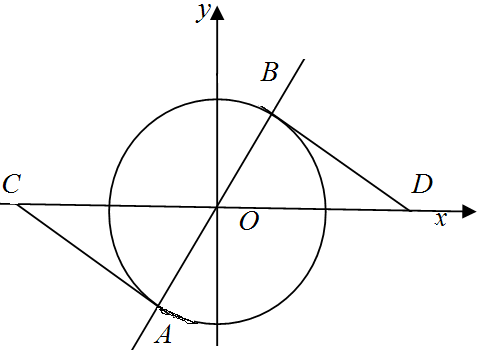 解:由圆的方程x2+y2=(2$\sqrt{3}$)2可知:圆心为(0,0),半径r=2$\sqrt{3}$,
解:由圆的方程x2+y2=(2$\sqrt{3}$)2可知:圆心为(0,0),半径r=2$\sqrt{3}$,
∵弦长为|AB|=4$\sqrt{3}$=2r,说明,直线过圆心.
则有:0=k(0-1)-$\sqrt{3}$,解得k=$\sqrt{3}$,
直线AB的方程为:y=$\sqrt{3}$x.
设直线AB的倾斜角为θ,则tanθ=$\sqrt{3}$,
∴θ=60°
Rt△AOC中:|CO|=$\frac{|OA|}{cos60°}$=$\frac{2\sqrt{3}}{\frac{1}{2}}$=4$\sqrt{3}$
那么:|CD|=2|OC|=8$\sqrt{3}$
故答案为:8$\sqrt{3}$.
点评 本题考查了直线与圆的位置关系的运用,弦长的问题.是中档题.

练习册系列答案
相关题目
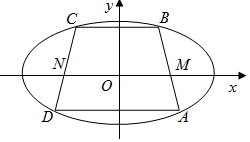 如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$
如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$