题目内容
己知等差数列{an}的首项为a1,公差为d,其前n项和为Sn,若直线y=a1x与圆(x-2)2+y2=4的两个交点关于直线x+y+d=0对称,则Sn= .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由直线和圆的知识易得a1和d,再由等差数列的求和公式可得.
解答:
解:∵直线y=a1x与圆(x-2)2+y2=4的两个交点关于直线x+y+d=0对称,
∴直线x+y+d=0过圆(x-2)2+y2=4的圆心(2,0),
∴2+d=0,解得d=-2;
又直线x+y+d=0的斜率是-1,∴a1=1,
∴Sn=na1+
d=2n-n2,
故答案为:2n-n2
∴直线x+y+d=0过圆(x-2)2+y2=4的圆心(2,0),
∴2+d=0,解得d=-2;
又直线x+y+d=0的斜率是-1,∴a1=1,
∴Sn=na1+
| n(n-1) |
| 2 |
故答案为:2n-n2
点评:本题考查等差数列的求和公式,涉及直线和圆的位置关系,属基础题.

练习册系列答案
相关题目
下列命题的说法错误的是( )
| A、命题“若x2-4x-3=0,则x=1”的逆否命题为“若x≠1,则x2-4x-3≠0” | ||||
| B、已知a,b,c是△A BC的三条边,△A BC是等边三角形的充要条件是a2+b2+c2=ab+ac+bc | ||||
C、命题“若α=
| ||||
| D、若命题p:b=0,命题q:函数f(x)=ax2+bx+c是偶函数,则p是q的充分不必要条件 |
如图是函数y=f(x)的导函数的图象,则正确的判断是( )
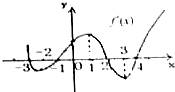

| A、f(x)在(-2,1)上是增函数 |
| B、x=1是f(x)的极大值点 |
| C、f(x)在(-1,2)上是增函数,在(2,4)上是减函数 |
| D、x=3是f(x)的极小值点 |
甲、乙、丙三位同学站成一排照相留念,则甲、乙相邻的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
