题目内容
已知函数f（x）=x（x-m）3在x=2处取得极小值，则常数m的值为（ ）
| A、2 | B、8 |
| C、2或8 | D、以上答案都不对 |
考点：利用导数研究函数的极值
专题：计算题,导数的概念及应用
分析：通过对函数f（x）求导，根据函数在x=2处有极值，可知f'（2）=0，解得m的值，再验证可得结论．
解答：
解：求导函数，可得f′（x）=（4x-m）（x-m）2，
∵在x=2处取得的极小值，
∴f′（2）=（8-m）（2-m）2=0，
∴m=2或8，
m=2时，f′（x）≥0，在x=2处不取极值，舍去，
m=8时，函数f（x）=x（x-m）3在x=2处取得极小值．
故选：B．
∵在x=2处取得的极小值，
∴f′（2）=（8-m）（2-m）2=0，
∴m=2或8，
m=2时，f′（x）≥0，在x=2处不取极值，舍去，
m=8时，函数f（x）=x（x-m）3在x=2处取得极小值．
故选：B．
点评：本题考查了函数的极值问题，考查学生的计算能力，正确理解极值是关键．
练习册系列答案
相关题目
函数y=πx+1的值域是（ ）
| A、（1，+∞） | B、[1，+∞） |
| C、R | D、（-∞，1） |
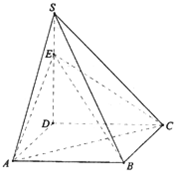如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=a，点E是SD上的点，且DE=λa（0＜λ≤1）．请利用空间向量解决下列问题：