题目内容
12．定义在[-2，2]上的偶函数f（x）在[-2，0]上是减函数，若f（x+1）＜f（2x），则实数x的取值范围是-1≤x＜-$\frac{1}{3}$．分析 先确定函数f（x）在[0，2]上是增函数，再将不等式转化为f（|x+1|）＜f（2x），即可求得x的取值范围．
解答 解：∵函数f（x）是定义在[-2，2]上的偶函数f（x）在[-2，0]上是减函数，
∴函数f（x）在[0，2]上是增函数，
∵f（x+1）＜f（2x），
∴f（|x+1|）＜f（|2x|），
∴|x+1|＜|2x|≤2，
∴-1≤x＜-$\frac{1}{3}$
故答案为：-1≤x＜-$\frac{1}{3}$．
点评 本题考查的知识点是函数奇偶性与单调性的综合应用，确定函数f（x）在[0，2]上是增函数，等价转化不等式是关键．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
9．
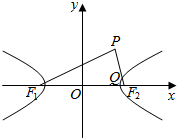如图，已知F1、F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左、右焦点，点P在第一象限，且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$，（$\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，线段PF2与双曲线C交于点Q，若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$，则双曲线C的渐近线方程为（ ）
如图，已知F1、F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左、右焦点，点P在第一象限，且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$，（$\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，线段PF2与双曲线C交于点Q，若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$，则双曲线C的渐近线方程为（ ）| A． | y=±$\frac{\sqrt{5}}{5}x$ | B． | y=±$\frac{1}{2}x$ | C． | y=±$\frac{\sqrt{3}}{2}x$ | D． | y=±$\frac{\sqrt{3}}{3}x$ |