题目内容
2.在△ABC中,AB=4,BC=6$\sqrt{2}$,∠CBA=$\frac{π}{4}$,.若双曲线Γ以AB为实轴,且过点C,则Γ的焦距为8.分析 由题意画出图形,求出C的坐标,代入双曲线方程求得b2的值,再结合隐含条件得答案.
解答 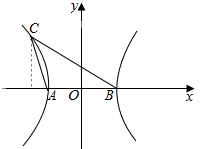 解:如图,设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$,
解:如图,设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$,
则由题意,2a=4,a=2,
在△ABC中,AB=4,BC=6$\sqrt{2}$,∠CBA=$\frac{π}{4}$,
∴C的横坐标为-($\frac{\sqrt{2}}{2}BC$-2)=-4,纵坐标为$\frac{\sqrt{2}}{2}BC=6$.
∵双曲线过点C,
则$\frac{16}{4}-\frac{36}{{b}^{2}}=1$,解得:b2=12,
∴c2=a2+b2=16,c=4.
则Γ的焦距为8.
故答案为:8.
点评 本题考查双曲线的定义,考查了双曲线的简单性质,是中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目