题目内容
【题目】在平面直角坐标系
中，已知定点
，点
在
轴上运动，点
在
轴上运动，点
为坐标平面内的动点，且满足
，
.
（1）求动点的轨迹
的方程；
（2）过曲线第一象限上一点
（其中
）作切线交直线
于点
，连结
并延长交直线于点
，求当
面积取最小值时切点
的横坐标.
【答案】（1）
；（2）
【解析】
（1）设点
，
，
，由已知条件推导出点
，
，由此能求出动点
的轨迹
的方程；
（2）分别求出切线
与
的方程，求得
，
的纵坐标，写出三角形的面积，利用导数求解当△
面积取最小值时切点
的横坐标．
解：（1）设
，
，
.因为
，
，
所以
，
，
，所以.
（2）
或
或
因为
为曲线上第一象限的点，则
过（其中
）作曲线的切线，则切线的斜率
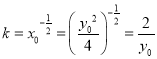
所以切线：
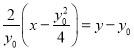，将
代入得
，
直线：
，将代入得
，
，
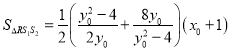因为在抛物线上且在第一象限，所以
，所以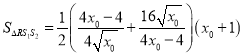
，
设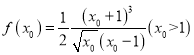
，
，
，
，
.
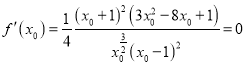练习册系列答案
相关题目
