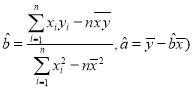题目内容
【题目】如图1,平面五边形![]() 是由边长为2的正方形
是由边长为2的正方形![]() 与上底为1,高为
与上底为1,高为![]() 直角梯形
直角梯形![]() 组合而成,将五边形
组合而成,将五边形![]() 沿着
沿着![]() 折叠,得到图2所示的空间几何体,其中
折叠,得到图2所示的空间几何体,其中![]() .
.
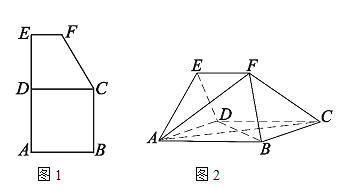
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(Ⅰ)以![]() 为原点,以平行于
为原点,以平行于![]() 的方向为
的方向为![]() 轴,平行于
轴,平行于![]() 的方向为
的方向为![]() 轴,建立空间直角坐标系.过
轴,建立空间直角坐标系.过![]() 点作
点作![]() 的高,交
的高,交![]() 于点
于点![]() ,先证明出
,先证明出![]() 平面
平面![]() ,设
,设![]() ,根据
,根据![]() ,可求出
,可求出![]() ,再利用向量法证明线线垂直,进而得到线面垂直;
,再利用向量法证明线线垂直,进而得到线面垂直;
(2)求出平面ABE的法向量![]() 、平面BCF的法向量
、平面BCF的法向量![]() ,由
,由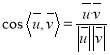 即可求出线面角.
即可求出线面角.
(1)以![]() 为原点,以平行于
为原点,以平行于![]() 的方向为
的方向为![]() 轴,平行于
轴,平行于![]() 的方向为
的方向为![]() 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.
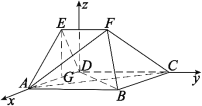
过![]() 点作
点作![]() 的高,交
的高,交![]() 于点
于点![]() .
.
由于![]() ,
,![]() ,
,![]()
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
设![]() ,由题设条件可得下列坐标:
,由题设条件可得下列坐标:
![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,由于
,由于![]() ,
,
所以![]() ,解得
,解得![]() ,
,
故![]() ,
,![]() .
.
可求![]() ,
,
且![]() ,
,![]() ,
,
从而![]() ,
,![]() .
.
因为![]() 平面
平面![]() ,且
,且![]() ,
,
故![]() 平面
平面![]() ;
;
(2)由(1)得![]() ,
,![]() ,
,![]() ,
,![]() .设平面
.设平面![]() 的法向量
的法向量![]() ,
,
由![]() 及
及![]() 得
得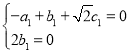
令![]() ,由此可得
,由此可得![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
由![]() 及
及![]() 得
得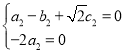
令![]() ,由此可得
,由此可得![]() .
.
则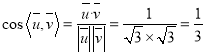 ,因为二面角
,因为二面角![]() 大于
大于![]() ,
,
则二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】下表是某公司2018年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:
月 份 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
研发费用(百万元) | 2 | 3 | 6 | 10 | 21 | 13 | 15 | 18 |
产品销量(万台) | 1 | 1 | 2 | 2.5 | 6 | 3.5 | 3.5 | 4.5 |
(Ⅰ)根据数据可知![]() 与
与![]() 之间存在线性相关关系,求出
之间存在线性相关关系,求出![]() 与
与![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(Ⅱ)该公司制定了如下奖励制度:以![]() (单位:万台)表示日销售,当
(单位:万台)表示日销售,当![]()
![]() 时,每位员工每日奖励200元;当
时,每位员工每日奖励200元;当![]() 时,每位员工每日奖励300元;当
时,每位员工每日奖励300元;当![]() 时,每位员工每日奖励400元.现已知该公司某月份日销售
时,每位员工每日奖励400元.现已知该公司某月份日销售![]() (万台)服从正态分布
(万台)服从正态分布![]() (其中
(其中![]() 是2018年5-12月产品销售平均数的二十分之一),请你估计每位员工该月(按30天计算)获得奖励金额总数大约多少元.
是2018年5-12月产品销售平均数的二十分之一),请你估计每位员工该月(按30天计算)获得奖励金额总数大约多少元.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数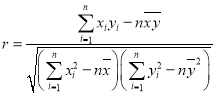 ,其回归直线
,其回归直线![]() 中的
中的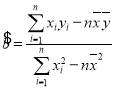 ,若随机变量
,若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .
.