题目内容
3．已知角α的终边在直线y=3x上，求sinα和cosα的值．分析 解方程组可得直线和单位圆的交点，由三角函数定义可得．
解答 解：联立$\left\{\begin{array}{l}{y=3x}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$可解得$\left\{\begin{array}{l}{x=\frac{\sqrt{10}}{10}}\\{y=\frac{3\sqrt{10}}{10}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{\sqrt{10}}{10}}\\{y=-\frac{3\sqrt{10}}{10}}\end{array}\right.$，
∴角α的终边和单位圆的交点为P（$\frac{\sqrt{10}}{10}$，$\frac{3\sqrt{10}}{10}$）和P′（-$\frac{\sqrt{10}}{10}$，-$\frac{3\sqrt{10}}{10}$），
当交点为P（$\frac{\sqrt{10}}{10}$，$\frac{3\sqrt{10}}{10}$）时，由三角函数定义可得sinα=y=$\frac{3\sqrt{10}}{10}$，cosα=x=$\frac{\sqrt{10}}{10}$；
当交点为P′（-$\frac{\sqrt{10}}{10}$，-$\frac{3\sqrt{10}}{10}$）时，由三角函数定义可得sinα=y=-$\frac{3\sqrt{10}}{10}$，cosα=x=-$\frac{\sqrt{10}}{10}$．
点评 本题考查三角函数的定义，涉及方程组的解法和分类讨论，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
15．定义在R上的函数f（x）、g（x）满足：对任意的实数x都有f（x）=f（|x|），g（-x）+g（x）=0，当x＞0时．f′（x）＞0，g′（x）＜0，则当x＜0时，有（ ）
| A． | f′（x）＞0，g′（x）＞0 | B． | f′（x）＞0，g′（x）＜0 | C． | f′（x）＜0，g′（x）＜0 | D． | f′（x）＜0，g′（x）＞0 |
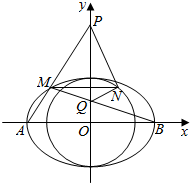已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）过点（{2，\sqrt{2}}）$，其焦点在⊙O：x2+y2=4上，A，B是椭圆的左右顶点．