题目内容
15.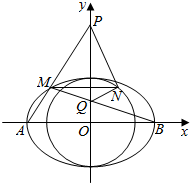 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})过点({2,\sqrt{2}})$,其焦点在⊙O:x2+y2=4上,A,B是椭圆的左右顶点.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})过点({2,\sqrt{2}})$,其焦点在⊙O:x2+y2=4上,A,B是椭圆的左右顶点.(Ⅰ)求椭圆C的方程;
(Ⅱ)M,N分别是椭圆C和⊙O上的动点(M,N不在y轴同侧),且直线MN与y轴垂直,直线AM,BM分别与y轴交于点P,Q,求证:PN⊥QN.
分析 (Ⅰ)由题意可得焦点为(±2,0),可得c=2,由点满足椭圆方程,即可得到所求方程;
(Ⅱ)令M(m,t),N(n,t),(m<0,n>0),可得m2+2t2=8,n2+t2=4,设P(0,p),Q(0,q),运用三点共线,可得p,q,再由两直线垂直的条件:斜率之积为-1,化简整理即可得证.
解答 解:(Ⅰ)由题意可得焦点为(±2,0),
可得c=2,即a2-b2=4,
又$\frac{4}{{a}^{2}}$+$\frac{2}{{b}^{2}}$=1,
解得a=2$\sqrt{2}$,b=2,
即有椭圆的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(Ⅱ)证明:令M(m,t),N(n,t),(m<0,n>0),
可得m2+2t2=8,n2+t2=4,
可得A(-2$\sqrt{2}$,0),B(2$\sqrt{2}$,0),
设P(0,p),Q(0,q),
由A,M,P三点共线可得kAM=kAP,
即有$\frac{t}{m+2\sqrt{2}}$=$\frac{p}{2\sqrt{2}}$,可得p=$\frac{2\sqrt{2}t}{m+2\sqrt{2}}$;
由B,M,Q三点共线可得kBM=kBQ,
即有$\frac{t}{m-2\sqrt{2}}$=$\frac{q}{-2\sqrt{2}}$,可得q=$\frac{-2\sqrt{2}t}{m-2\sqrt{2}}$.
由kPN•kQN=$\frac{t-\frac{2\sqrt{2}t}{m+2\sqrt{2}}}{n}$•$\frac{t-\frac{-2\sqrt{2}t}{m-2\sqrt{2}}}{n}$
=$\frac{{m}^{2}{t}^{2}}{{n}^{2}({m}^{2}-8)}$,
由m2+2t2=8,n2+t2=4,可得m2-8=-2t2,
n2=4-t2,m2=2(4-t2),即为m2=2n2,
可得$\frac{{m}^{2}{t}^{2}}{{n}^{2}({m}^{2}-8)}$=$\frac{2{t}^{2}}{-2{t}^{2}}$=-1,
即有PN⊥QN.
点评 本题考查椭圆的方程的求法,注意运用点满足椭圆方程,考查两直线垂直的条件:斜率之积为-1,以及三点共线的条件:斜率相等,考查化简整理的运算能力,属于中档题.

| A. | $({0,\frac{4}{27}})$ | B. | $({0,\frac{4}{27}}]$ | C. | $({\frac{4}{27},\frac{2}{3}})$ | D. | $({\frac{4}{27},\frac{2}{3}}]$ |