题目内容
11.将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{8}$个单位,得到函数g(x)的图象,则函数g(x)的解析式为g(x)=sin2x.分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{8}$个单位,得到函数g(x)=sin[2(x-$\frac{π}{8}$)+$\frac{π}{4}$]=sin2x的图象,
则函数g(x)的解析式为g(x)=sin2x,
故答案为:sin2x.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
2.已知函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象与直线y=m(-A<m<0)的三个相邻交点的横坐标分别是3,5,9,则f(x)的单调递增区间是( )
| A. | [6kπ+1,6kπ+4],k∈Z | B. | [6k-2,6k+1],k∈Z | C. | [6k+1,6k+4],k∈Z | D. | [6kπ-2,6kπ+1],k∈Z |
20.已知平面向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(-2,2),则$\overrightarrow{a}$+2$\overrightarrow{b}$=( )
| A. | (3,4) | B. | (-3,2) | C. | (-1,0) | D. | (5,-6) |
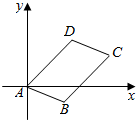 如图,已知平行四边形ABCD的三个顶点的坐标分别为A(0,0),B(2,-1),C(4,2).
如图,已知平行四边形ABCD的三个顶点的坐标分别为A(0,0),B(2,-1),C(4,2).