题目内容
设函数y=f(x)是定义在(0,+∞)上的函数,并且满足下面三个条件:
①对任意正数x,y,都有f(xy)=f(x)+f(y);
②当x>1时,f(x)<0;
③f(3)=-1.
(Ⅰ)求f(1)、f(
)的值;
(Ⅱ)证明:f(x)在(0,+∞)上是减函数.
①对任意正数x,y,都有f(xy)=f(x)+f(y);
②当x>1时,f(x)<0;
③f(3)=-1.
(Ⅰ)求f(1)、f(
| 1 |
| 9 |
(Ⅱ)证明:f(x)在(0,+∞)上是减函数.
考点:抽象函数及其应用
专题:计算题,证明题,函数的性质及应用
分析:(Ⅰ)令x=y=1,求出f(1)=0,令x=y=3求出f(9),令x=9,y=
,求出f(
);
(Ⅱ)0<x1<x2,则
>1,则由②得f(
)<0,再由①得到f(x2)<f(x1),由函数的单调性即可得证.
| 1 |
| 9 |
| 1 |
| 9 |
(Ⅱ)0<x1<x2,则
| x2 |
| x1 |
| x2 |
| x1 |
解答:
(Ⅰ)解:令x=y=1,得f(1)=2f(1),即f(1)=0,
而f(9)=f(3)+f(3)=-1-1=-2,
且f(9)+f(
)=f(1)=0,得f(
)=2.
(Ⅱ)证明:若0<x1<x2,则
>1,
则由②得f(
)<0,
∴f(x2)=f(
•x1)=f(
)+f(x1)<f(x1),
∴f(x)在(0,+∞)上是减函数.
而f(9)=f(3)+f(3)=-1-1=-2,
且f(9)+f(
| 1 |
| 9 |
| 1 |
| 9 |
(Ⅱ)证明:若0<x1<x2,则
| x2 |
| x1 |
则由②得f(
| x2 |
| x1 |
∴f(x2)=f(
| x2 |
| x1 |
| x2 |
| x1 |
∴f(x)在(0,+∞)上是减函数.
点评:本题考查函数的单调性和运用,考查抽象函数值的求法:赋值法.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
关于x的不等式x2-2ax-8a2<0的解集为(x1,x2),且x12-x22=15,则实数a=( )
A、
| ||||||||
B、-
| ||||||||
C、-
| ||||||||
D、-
|
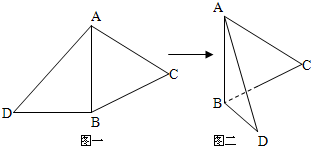 如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成直二面角D-AB-C,如图二,在二面角D-AB-C中.
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成直二面角D-AB-C,如图二,在二面角D-AB-C中. 如图,在四棱锥E-ABCD中,AB⊥平面BCE,DC⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=
如图,在四棱锥E-ABCD中,AB⊥平面BCE,DC⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=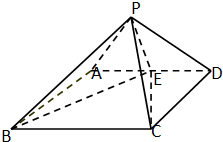 如图,四棱锥P-ABCD的底面是矩形,侧面PAD⊥底面ABCD,在△PAD中
如图,四棱锥P-ABCD的底面是矩形,侧面PAD⊥底面ABCD,在△PAD中