题目内容
 如图,在四棱锥E-ABCD中,AB⊥平面BCE,DC⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=
如图,在四棱锥E-ABCD中,AB⊥平面BCE,DC⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=| 2π |
| 3 |
( I)求证:平面ADE⊥平面ABE;
(Ⅱ)求二面角A-EB-D的大小.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)取BE的中点O,连OC,OF,DF,可利用条件得OC∥FD,再利用条件证得OC⊥平面ABE,即可得到平面ADE⊥平面ABE;
(Ⅱ)因为二面角A-EB-D与二面角F-EB-D相等,即找二面角F-EB-D的平面角为∠FOD即可.
(Ⅱ)因为二面角A-EB-D与二面角F-EB-D相等,即找二面角F-EB-D的平面角为∠FOD即可.
解答:
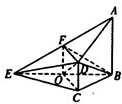 (Ⅰ)证明:取BE的中点O,连OC,OF,DF,则2OF与BA平行且相等.
(Ⅰ)证明:取BE的中点O,连OC,OF,DF,则2OF与BA平行且相等.
∵AB⊥平面BCE,CD⊥平面BCE,∴2CD与BA平行且相等,
∴OF与CD平行且相等,
∴OC∥FD;
∵BC=CE,∴OC⊥BE,
又AB⊥平面BCE.
∴OC⊥平面ABE.∴FD⊥平面ABE.
从而平面ADE⊥平面ABE;
(Ⅱ)解:二面角A-EB-D与二面角F-EB-D相等,
由(Ⅰ)知二面角F-EB-D的平面角为∠FOD.
BC=CE=2,∠BCE=120°,OC⊥BE得BO=OE=
,OC=1,
∴OFDC为正方形,
∴∠FOD=45°.
 (Ⅰ)证明:取BE的中点O,连OC,OF,DF,则2OF与BA平行且相等.
(Ⅰ)证明:取BE的中点O,连OC,OF,DF,则2OF与BA平行且相等.∵AB⊥平面BCE,CD⊥平面BCE,∴2CD与BA平行且相等,
∴OF与CD平行且相等,
∴OC∥FD;
∵BC=CE,∴OC⊥BE,
又AB⊥平面BCE.
∴OC⊥平面ABE.∴FD⊥平面ABE.
从而平面ADE⊥平面ABE;
(Ⅱ)解:二面角A-EB-D与二面角F-EB-D相等,
由(Ⅰ)知二面角F-EB-D的平面角为∠FOD.
BC=CE=2,∠BCE=120°,OC⊥BE得BO=OE=
| 3 |
∴OFDC为正方形,
∴∠FOD=45°.
点评:本题考查平面与平面垂直的证明,考查二面角的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
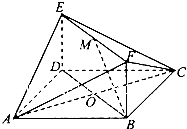 如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=
如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=