题目内容
5. 如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为$\frac{2π}{3}$+4.
如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为$\frac{2π}{3}$+4.
分析 几何体为两个半圆锥与一个四棱柱的组合体,求出各部分的体积再相加即可.
解答 解:由三视图可知几何体为两个半圆锥与一个长方体的组合体.
半圆锥的底面半径r=1,高为2,长方体的棱长为1,2,2,
∴几何体的体积V=$\frac{1}{3}π×{1}^{2}$×2+1×2×2=$\frac{2π}{3}$+4.
故答案为$\frac{2π}{3}$+4.
点评 本题考查了常见几何体的三视图及体积计算,属于中档题.

练习册系列答案
相关题目
16.已知函数f(x)=2x,等差数列{an}的公差为2.若f(a2+a4+a6+a8+a10)=4,则log2[f(a1)•f(a2)•f(a3)•…•f(a10)]=( )
| A. | 8 | B. | 4 | C. | -6 | D. | $\frac{1}{4}$ |
13.如图,小方格是边长为1的正方形,一个几何体的三视图如图,则几何体的表面积为( )
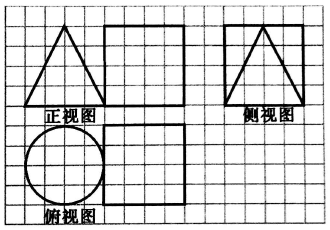

| A. | 4$\sqrt{5}π+96$ | B. | (2$\sqrt{5}+6$)π+96 | C. | (4$\sqrt{5}+4$)π+64 | D. | (4$\sqrt{5}$+4)π+96 |
20.已知命题p:?x∈(-∞,0),2x<3x;命题q:?x∈(0,$\frac{π}{2}$),sinx<x,则下列命题为真命题的是( )
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
10.设{an}是首项为a1,公比为q的等比数列,则“a1q>0”是“{an}为递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知公差不为0的等差数列{an}满足a1,a3,a4成等比数列,Sn为数列{an}的前n项和,则$\frac{{{S_4}-{S_2}}}{{{S_5}-{S_3}}}$的值为( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
14.已知数列{an}的前n项和为Sn,a1=1,an+1=3Sn+2,则a4=( )
| A. | 64 | B. | 80 | C. | 256 | D. | 320 |
6.已知0<a<1<b,函数f(x)=lg(bax-abx)定义域为(-1,1),值域为(-∞,0),则a(b-$\frac{3}{2}$)的取值范围是( )
| A. | ($\frac{1-\sqrt{5}}{4}$,0) | B. | ($\frac{1-\sqrt{5}}{4}$,$\frac{\sqrt{5}-2}{2}$) | C. | [$\frac{9-9\sqrt{5}}{32}$,$\frac{\sqrt{5}-2}{2}$) | D. | [$\frac{9-9\sqrt{5}}{32}$,0) |
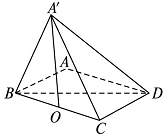 如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.
如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.