题目内容
与曲线ρcosθ+1=0关于θ=
对称的曲线的极坐标方程是 ．
| π |
| 4 |
考点：简单曲线的极坐标方程
专题：计算题
分析：先将原极坐标方程ρcosθ+1=0化成直角坐标方程，再结合曲线关于直线的对称性，利用直角坐标方程解决问题．
解答：
解：将原极坐标方程ρcosθ+1=0，
化成直角坐标方程为：x+1=0，
它关于直线y=x（即 θ=
）对称的圆的方程是
y+1=0，其极坐标方程为：ρsinθ+1=0
故答案为：ρsinθ+1=0．
化成直角坐标方程为：x+1=0，
它关于直线y=x（即 θ=
| π |
| 4 |
y+1=0，其极坐标方程为：ρsinθ+1=0
故答案为：ρsinθ+1=0．
点评：本题考查点的极坐标和直角坐标的互化，利用直角坐标与极坐标间的关系：ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．
练习册系列答案
相关题目
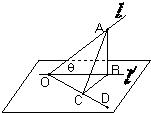如图，l是平面α的斜线，斜足是O，A是l上任意一点，AB是平面α的垂线，B是垂足，设OD是平面α内与OB不同的一条直线，AC垂直于OD于C，若直线l与平面α所成的角θ=45°，∠BOC=45°，求∠AOC的大小．空间四个不同的平面，它们有多种位置关系，从交线数目看，所有可能出现的交线数目的集合是（ ）
| A、{0，1，2，3，4，5，6} |
| B、{0，1，3，4，5，6} |
| C、{0，1，2，3，5，6} |
| D、{0，1，3，4} |
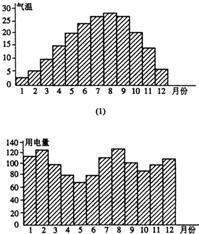一般地，家庭用电量y（千瓦）与气温x（℃）有函数关系y=f（x）．图（1）表示某年12月中每月的平均气温，图（2）表示某家庭在12个月中每月的用电量．试在数集A={x|5≤x≤30，x是2.5的整数倍}中确定一个最小值x1和最大值x2，使y=f（x）是[x1，x2]上的增函数，则区间[x1，x2]=