Question

已知关于x的一次函数y=mx+n．
（1）设集合P={-4，-1，1，2，3}和Q={-4，3}，分别从集合P和Q中随机取一个数作为m和n，求函数y=mx+n是减函数的概率；
（2）实数m，n满足条件

m+n-1≤0 -1≤m≤1 -1≤n≤1

求函数y=mx+n的图象经过一、二、四象限的概率．

Answer 1

考点：几何概型,列举法计算基本事件数及事件发生的概率

专题：概率与统计

分析：（1）由题意，写出所有满足条件的事件，由古典概型公式解答；
（2）画出平面区域，计算区域面积，由几何概型的公式解答．

解答： 解：（1）由已知，抽取的全部结果表示为（m，n），则基本事件有：（-4，-4），（-4，3），（-1，-4），（-1，3），（1，-4），（1，3），（2，-4），（2，3），（3，-4），（3，3），共10个基本事件，设使函数为减函数的事件为A，m＜0，则A包含的基本事件有：（-4，-4），（-4，3），（-1，-4），（-1，3），共4个基本事件，由古典概型公式，P（A）=

4

10

=

2

5

．…（7分）
（2）m、n满足条件

m+n-1≤0 -1≤m≤1 -1≤n≤1

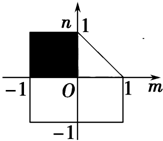
的区域如图所示：
要使函数的图象过一、二、四象限，则m＜0，n＞0，故使函数图象过一、二、四象限的（m，n）的区域为第二象限的阴影部分，
由几何概型的概率公式得所求事件的概率为P=

1

7 2

=

2

7

．…（14分）

点评：本题考查了古典概型、几何概型的公式的运用；古典概型关键是明确事件的个数；几何概型关键是明确事件的测度，然后由公式解答．