题目内容
直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:画出图形,找出BM与AN所成角的平面角,利用解三角形求出BM与AN所成角的余弦值.
解答:
 解:直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,如图:BC 的中点为O,连结ON,
解:直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,如图:BC 的中点为O,连结ON,
MN
B1C1=OB,则MN0B是平行四边形,BM与AN所成角就是∠ANO,
∵BC=CA=CC1,
设BC=CA=CC1=2,∴CO=1,AO=
,AN=
,MB=
=
=
,
在△ANO中,由余弦定理可得:cos∠ANO=
=
=
.
故选:C.
 解:直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,如图:BC 的中点为O,连结ON,
解:直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,如图:BC 的中点为O,连结ON,MN
| ∥ |
. |
| 1 |
| 2 |
∵BC=CA=CC1,
设BC=CA=CC1=2,∴CO=1,AO=
| 5 |
| 5 |
| B1M2+BB12 |
(
|
| 6 |
在△ANO中,由余弦定理可得:cos∠ANO=
| AN2+NO2-AO2 |
| 2AN•NO |
| 6 | ||||
2×
|
| ||
| 10 |
故选:C.
点评:本题考查异面直线对称角的求法,作出异面直线所成角的平面角是解题的关键,同时考查余弦定理的应用.

练习册系列答案
相关题目
设b、c分别是先后抛掷一枚骰子得到的点数,则函数f(x)=x2+bx+c有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设实数x,y满足不等式组
,若x,y为整数,则3x+4y的最大值是( )
|
| A、26 | B、25 | C、23 | D、22 |
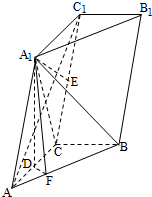 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.