题目内容
17.已知函数$f(x)=\frac{1}{x}+alnx(a为参数)$(1)若a=1,求函数f(x)的单调区间;
(2)当x∈(0,e]时,求函数f(x)的最小值;
(3)求证:${(1+\frac{1}{n})^n}<e<{(1+\frac{1}{n})^{n+1}}(n∈{N^*})$.
分析 (1)a=1时,在定义域内解不等式f′(x)>0,f′(x)<0即可;
(2)分情况进行讨论:a≤0时易判断单调性,由单调性可得最小值;a>0时,按照极值点$\frac{1}{a}$与区间(0,e]的位置关系再分两种情况讨论,由单调性可求;
(3)对(1+$\frac{1}{n}$)n<e<(1+$\frac{1}{n}$)n+1两边取对数,可整理为 $\frac{1}{n+1}$<ln(1+$\frac{1}{n}$)<$\frac{1}{n}$,令x=1+$\frac{1}{n}$,只要证1-$\frac{1}{x}$<lnx<x-1,(1<x≤2),左边不等式可由(1)问结论得到;右边不等式通过构造函数利用导数可证明.
解答 解:(1)$f'(x)=-\frac{1}{x^2}+\frac{a}{x}=\frac{ax-1}{x^2}$(x>0),
当a=1时,$f'(x)=\frac{x-1}{x^2}$,令f'(x)=0,得x=1,
当x变化时,f'(x),f(x)变化如下:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
(2)①当a≤0时,f'(x)<0,f(x)在(0,e]上递减,${y_{min}}=f(e)=\frac{1}{e}+a$
②当$\frac{1}{a}≥e$时,即$0<a≤\frac{1}{e}$时,f'(x)<0,f(x)在(0,e]上递减,${y_{min}}=f(e)=\frac{1}{e}+a$
③当$0<\frac{1}{a}<e$时,即$a>\frac{1}{e}$时,当x变化时,f'(x),f(x)变化如下:
| x | (0,$\frac{1}{a}$) | $\frac{1}{a}$ | ($\frac{1}{a}$,e) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
综上,$f{(x)_{min}}=\left\{\begin{array}{l}a+\frac{1}{e},(a≤\frac{1}{e})\\ a+aln\frac{1}{a},(a>\frac{1}{e})\end{array}\right.$;
(3)对${(1+\frac{1}{n})^n}<e<{(1+\frac{1}{n})^{n+1}}$两边取对数得,
$nln(1+\frac{1}{n})<1<(n+1)ln(1+\frac{1}{n})$,即$\frac{1}{n+1}<ln(1+\frac{1}{n})<\frac{1}{n}$,
只需证 $\frac{1}{n+1}<ln(1+\frac{1}{n})<\frac{1}{n}$,令$x=1+\frac{1}{n}$,
只需证$1-\frac{1}{x}<lnx<x-1(1<x≤2)$,
证明如下:由(1)知 a=1时,$f(x)=lnx+\frac{1}{x}(x>0)$的最小值为f(1),
所以$f(x)=lnx+\frac{1}{x}≥f(1)=1$,
即 $1-\frac{1}{x}≤lnx$,又因为1<x≤2,上式等号取不到,所以$1-\frac{1}{x}<lnx$①,
令g(x)=x-lnx-1(1<x≤2),则$g'(x)=1-\frac{1}{x}=\frac{x-1}{x}>0$,
∴g(x)在1<x≤2上是增函数,∴g(x)>g(1)=0②,
综合①②得$\frac{x}{x+1}<ln(x+1)<x(1<x≤2)$,
即$\frac{1}{n+1}<ln(1+\frac{1}{n})<\frac{1}{n}$所以原命题得证.
点评 该题考查利用导数研究函数的单调性、最值、证明不等式,考查分类讨论思想,考查学生分析问题解决问题的能力,综合性强,难度大,解决(3)问的关键是通过去对数对原不等式进行合理变形.

练习册系列答案
相关题目
5.已知x<0,则$y=3x+\frac{4}{x}$有( )
| A. | 最大值$-4\sqrt{3}$ | B. | 最小值$-4\sqrt{3}$ | C. | 最大值$4\sqrt{3}$ | D. | 最小值$4\sqrt{3}$ |
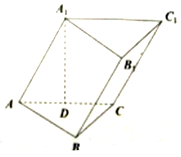 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.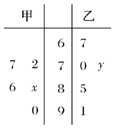 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);