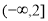题目内容
2.函数y=-$\frac{2}{3}$x3+(a+$\frac{1}{a}$)x2-2x+4(a<-1)的递减区间为(a,$\frac{1}{a}$).分析 先求出函数的导数,通过导函数,求解导函数值为负数时,求出函数的单调递减区间.
解答 解:函数y=-$\frac{2}{3}$x3+(a+$\frac{1}{a}$)x2-2x+4(a<-1)
可得y′=-2x2+2ax+$\frac{2}{a}$x-2=-2(x-a)(x-$\frac{1}{a}$),
令y′<0,得(x-a)(x-$\frac{1}{a}$)>0.
∵a<-1,∴a<-1$<\frac{1}{a}$<0,不等式解为x<a或x>$\frac{1}{a}$,
此时函数的单调递减区间为(a,$\frac{1}{a}$).
故答案为:(a,$\frac{1}{a}$).
点评 本题考查了函数的单调性,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
17.某程序框图如图所示,该程序运行结束时输出的S的值为( )


| A. | 1007 | B. | 1008 | C. | 2016 | D. | 3024 |
14.某考点2016年参加教师资格考试的人群由两部分组成,分别为在职人员与社会人员,现利用随机抽样的方法抽取50名参考人员研究它们的考试成绩,并将考试成绩和频数统计如下表所示:
将频率作为概率,解决下列问题:
(1)在这50名参考人员中任取一位,求分数不低于105分的概率;
(2)为了进一步了解这些参考人员的得分情况,再从分数在[65,75)的参考人员A,B,C中选出2位,从分数在[115,150)中的参考人员D,E,F,G,H中选出1位进行研究,求A和D同时被选到的概率.
| 组别 | [65,75) | [75,85) | [85,95) | [95,105) | [105,115) | [115,150) |
| 频数 | 3 | 4 | 13 | 15 | 10 | 5 |
(1)在这50名参考人员中任取一位,求分数不低于105分的概率;
(2)为了进一步了解这些参考人员的得分情况,再从分数在[65,75)的参考人员A,B,C中选出2位,从分数在[115,150)中的参考人员D,E,F,G,H中选出1位进行研究,求A和D同时被选到的概率.
12.下列说法正确的是( )
| A. | 都与直线a相交的两条直线确定一个平面 | |
| B. | 两条直线确定一个平面 | |
| C. | 过一条直线的平面有无数多个 | |
| D. | 两个相交平面的交线是一条线段 |
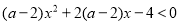 对一切
对一切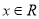 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )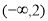 B.[-2,2] C.(-2,2] D.
B.[-2,2] C.(-2,2] D.