题目内容
12.焦点为(0,±6)且与双曲线$\frac{x^2}{2}-{y^2}=1$有相同渐近线的双曲线方程是( )| A. | $\frac{x^2}{12}-\frac{y^2}{24}=1$ | B. | $\frac{y^2}{12}-\frac{x^2}{24}=1$ | C. | $\frac{y^2}{24}-\frac{x^2}{12}=1$ | D. | $\frac{x^2}{24}-\frac{y^2}{12}=1$ |
分析 根据题意,由已知焦点坐标设要求双曲线的方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1,分析可得a2+b2=36①,由双曲线$\frac{x^2}{2}-{y^2}=1$的方程可得其渐近线方程,进而可得$\frac{a}{b}$=$\frac{\sqrt{2}}{2}$②,联立①②可得a2、b2的值,代入要求双曲线的方程,即可得答案.
解答 解:根据题意,要求双曲线的焦点为(0,±6),可以设其方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1,
若其焦点为(0,±6),即c=6,则有a2+b2=36,①
双曲线$\frac{x^2}{2}-{y^2}=1$的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,
则双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1的渐近线也为y=±$\frac{\sqrt{2}}{2}$x,则有$\frac{a}{b}$=$\frac{\sqrt{2}}{2}$,②
联立①②可得:a2=12,b2=24,
则要求双曲线的方程为:$\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1,
故选:B.
点评 本题考查双曲线的标准方程的求法,注意用待定系数法分析之前,确定双曲线焦点的位置.

练习册系列答案
相关题目
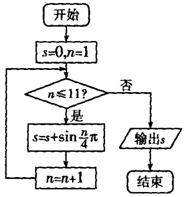
3.用秦九韶算法求多项式f(x)=x6+6x4+9x2+208在x=-4时,v2的值为( )
| A. | -4 | B. | 1 | C. | 17 | D. | 22 |
7.经过点A(1,1),并且在两坐标轴上的截距的绝对值相等的直线有( )
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 3条 |
17.在△ABC中,a,b,c分别为A,B,C的对边,已知a,b,c成等比数列,a2-c2=ac+bc,a=3$\sqrt{3}$,则$\frac{b+c}{sinB+sinC}$=( )
| A. | 12 | B. | 6$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 6 |
1.已知:a,b均为正数,4a+b=2ab,则使a+b≥c恒成立的c的取值范围是( )
| A. | (-∞,$\frac{9}{2}$] | B. | (-∞,1] | C. | (-∞,9] | D. | (-∞,8] |
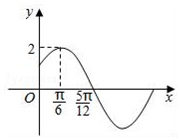 已知函数f(x)=Asin(ωx+φ)
已知函数f(x)=Asin(ωx+φ)