题目内容
1.已知:a,b均为正数,4a+b=2ab,则使a+b≥c恒成立的c的取值范围是( )| A. | (-∞,$\frac{9}{2}$] | B. | (-∞,1] | C. | (-∞,9] | D. | (-∞,8] |
分析 由题意知,要使a+b≥c恒成立,即a+b的最小值≥c,利用均值不等式求解即可.
解答 解:∵a,b均为正数,4a+b=2ab,
∴$\frac{1}{a}$+$\frac{4}{b}$=2,
∴a+b=$\frac{1}{2}$(a+b)($\frac{1}{a}$+$\frac{4}{b}$)=$\frac{1}{2}$(1+4+$\frac{b}{a}$+$\frac{4a}{b}$)≥$\frac{1}{2}$(5+4)=$\frac{9}{2}$,当且仅当b=2a时,取等号,
∴c≤$\frac{9}{2}$,
故选:A
点评 本题通过恒成立问题的形式,考查了均值不等式,灵活运用了“2”的代换,是高考考查的重点内容.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
12.焦点为(0,±6)且与双曲线$\frac{x^2}{2}-{y^2}=1$有相同渐近线的双曲线方程是( )
| A. | $\frac{x^2}{12}-\frac{y^2}{24}=1$ | B. | $\frac{y^2}{12}-\frac{x^2}{24}=1$ | C. | $\frac{y^2}{24}-\frac{x^2}{12}=1$ | D. | $\frac{x^2}{24}-\frac{y^2}{12}=1$ |
16.已知随机变量ξ~B(10,0.6),则E(ξ),D(ξ)分别是( )
| A. | 6和2.4 | B. | 4和2.4 | C. | 4和3.6 | D. | 6和1.6 |
17.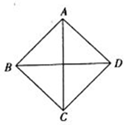 已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
 已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$+2 | D. | 4$\sqrt{3}$+2 |