题目内容
18.设F1,F2分别是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,点P在椭圆C上,若线段PF1的中点在y轴上,∠PF1F2=30°,F1F2=2,则椭圆的标准方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.分析 判断三角形PF1F2是直角三角形,依题意可求得|PF1|与|PF2|,求出a,然后求解b,即可求解椭圆方程.
解答 解:F1,F2分别是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,点P在椭圆C上,若线段PF1的中点在y轴上,可得PF2⊥F1F2,∠PF1F2=30°,
∴|F1F2|=2,|PF1|=$\frac{4\sqrt{3}}{3}$,|PF2|=$\frac{2\sqrt{3}}{3}$
又|PF1|+|PF2|=2a=2$\sqrt{3}$,a=$\sqrt{3}$,|F1F2|=2c=2,c=1,
∴b=$\sqrt{2}$.
所求椭圆方程为:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.
故答案为:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.
点评 本题考查椭圆的简单性质,求得|PF1|与|PF2|是关键,考查理解与应用能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知复数$\frac{1}{z}=({-2+i})({2i-1})$,则$\overline z$等于( )
| A. | $-\frac{i}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{i}{5}$ | D. | $\frac{1}{5}$ |
6.已知函数f(x),且f(x)=2x•f'(1)+lnx,则f'(1)=( )
| A. | -e | B. | -1 | C. | 1 | D. | e |
3.函数f(x)=mlnx-cosx在x=1处取到极值,则m的值为( )
| A. | sin1 | B. | -sin1 | C. | cos1 | D. | -cos1 |
8.设函数f(x)的导函数为f'(x),且满足$xf'(x)+f(x)=\frac{e^x}{x}$,f(1)=e,则x>0时,f(x)( )
| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既有极大值又有极小值 | D. | 既无极大值也无极小值 |
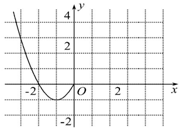 已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象(二次函数图象的一部分),如图所示,请根据图象:
已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象(二次函数图象的一部分),如图所示,请根据图象: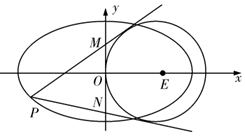 已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.
已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.