题目内容

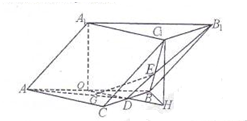
如图，在斜三棱柱ABC-A1B1C1中，点A1在底面ABC上的射影恰好是AB的中点O，底面ABC是正三角形，其重心为G点，D是BC中点，B1D交BC1于E．
（1）求证：GE∥侧面AA1B1B；
（2）若AA1=AB，求直线BC1与底面ABC所成角．
考点：直线与平面所成的角,直线与平面平行的判定
专题：空间角
分析：（1）由已知得
DE
EB1
=
BD
B1C1
=
1
2
，
DE
EB1
=
DG
GA
=
1
2
，从而GE∥AB1，由此能证明GE∥侧面AA1B1B．
（2）令AA1=AB=2，A1在底面ABC上的射影为AB中心O，连OD延长到H，使OD=DH，连C1H，BH，由A1C1
∥
.
OH，得A1O
∥
.
C1H，∠C1BH是直线BC1与底面ABC所成角，由此能求出直线BC1与底面ABC所成角．
解答： （1）证明：∵斜三棱柱ABC-A1B1C1中，
点A1在底面ABC上的射影恰好是AB的中点O，
底面ABC是正三角形，其重心为G点，D是BC中点，B1D交BC1于E，
∴
DE
EB1
=
BD
B1C1
=
1
2
，
连结AB1，则
DE
EB1
=
DG
GA
=
1
2
，
∴GE∥AB1，
∵GE不包含于侧面AA1B1B，AB1?侧面AA1B1B，
∴GE∥侧面AA1B1B．
（2）解：令AA1=AB=2，A1在底面ABC上的射影为AB中心O，
连OD延长到H，使OD=DH，连C1H，BH，
则由A1C1
∥
.
OH，得A1O
∥
.
C1H，
∠C1BH是直线BC1与底面ABC所成角
∴C1H=
3
，BH=OC=
3
，
∴tan∠C1HB=1，∴∠C1BH=
π
4
，
∴直线BC1与底面ABC所成角为
π
4
．
点评：本题考查直线与平面平行的证明，考查直线与底面所成的角的大小的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
一个袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，每个小球被取出的可能性都相等，按3个小球上最大数字的9倍计分．用X表示取出的3个小球上的最大数字．求：
（Ⅰ）取出的3个小球上的数字互不相同的概率；
（Ⅱ）随机变量X的分布列和均值；
（Ⅲ）计分介于20分到40分之间的概率．
设函数f（x）=x2-x+alnx，其中a≠0．
（1）a=-6，求函数f（x）在[1，4]上的最值；
（2）设函数f（x）既有极大值，又有极小值，求实数a的取值范围；
（3）求证：当n∈N*时，e n(n2-1)≥（n!）3．
已知函数f（x）=ln（2-x）+ax，a＞0，a∈R．
（1）设曲线y=f（x）在点（1，f（1））处的切线l平行于x轴，求a的值；
（2）求函数f（x）的单调区间；
（3）求函数f（x）的区间[0，1]上的最小值．
已知
a
=（2cosx，1），
b
=（cosx，
3
sin2x），且f（x）=
a
•
b
，
（1）求f（x）在x∈[-
π
3
，
π
3
]的最大值；
（2）若f（x）=1-
3
，x∈[-
π
3
，
π
3
]，求x；
（3）函数f（x）的图象可以由函数y=2sin2x的图象经过怎样的变换得出？
设数列{an}的前n项和为Sn，已知a1=a（a≠3，a∈R），an+1=Sn+3n，n∈N*
（Ⅰ）设bn=Sn-3n ，n∈N*，求{bn}的通项公式；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）若an+1≥a，n∈N*，求a的取值范围．
已知函数f（x）=alnx-x+
1
x
，g（x）=x2+x-b，y=f（x）图象恒过定点P，且P点既在y=g（x）图象上，又在y=f（x）的导函数的图象上．
（1）求a，b的值；
（2）设h（x）=
f(x)
g(x)
，求证：当x＞0且x≠1时，h（x）＜0．
袋中有一元人民币两枚，现依次有放回地随机摸取3次，每次摸一枚硬币．
（1）试问，一共有多少种不同的结果，列出所有可能的结果（其中正面朝上与反面朝上是不同的结果）
（2）若摸到正面朝上时得2分，摸到反面朝上得1分，求3次摸得总分为5分的概率．
关于图中的正方体ABCD-A1B1C1D1，下列说法正确的有：
 
．
①P点在线段BD上运动，棱锥P-AB1D1体积不变；
②P点在线段BD上运动，直线AP与平面A1B1C1D1平行；
③一个平面α截此正方体，如果截面是三角形，则必为锐角三角形；
④一个平面α截此正方体，如果截面是四边形，则必为平行四边形；
⑤平面α截正方体得到一个六边形（如图所示），则截面α在平面AB1D1与平面BDC1间平行移动时此六边形周长先增大，后减小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网