题目内容
函数f（x）=ax2+4（a-3）x+5在区间（-∞，2）上是减函数，则a的取值范围是 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：由条件利用二次函数的性质可得，当a=0时满足条件；当a≠0时，则由
求得a的范围．综合可得a的取值范围．
|
解答：
解：由于函数f（x）=ax2+4（a-3）x+5在区间（-∞，2）上是减函数，
当a=0时，f（x）=-12x+5，满足条件．
当a≠0时，则有
，解得0＜a≤
．
综上可得，0≤a≤
，
故答案为：[0，
]．
当a=0时，f（x）=-12x+5，满足条件．
当a≠0时，则有
|
| 3 |
| 2 |
综上可得，0≤a≤
| 3 |
| 2 |
故答案为：[0，
| 3 |
| 2 |
点评：本题主要考查二次函数的性质应用，体现了转化、分类讨论的数学思想，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}满足a1=2，an+1=
，则a2014等于（ ）
| 1+an |
| 1-an |
| A、2 | ||
| B、-3 | ||
C、-
| ||
D、
|
已知一个圆锥的地面半径为R，高为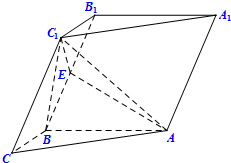
如图，在三棱柱ABC-A1B1C1中，已知AB⊥BB1C1C，BC=1，AB=BB1=2，∠BCC1=
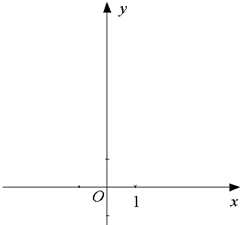已知函数f（x）=ax2+（a-1）x+b的最小值为-1，且f（0）=-1．
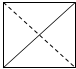在空间直角坐标系O xyz中，一个四面体的顶点坐标分别是（0，0，0），（1，0，1），（1，1，0），（0，1，1），且该四面体的俯视图如图，则左视图为（ ）
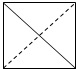
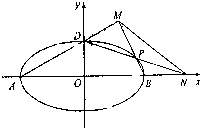已知椭圆若函数f（x）为定义在R上的奇函数，且在（0，+∞）内是增加的，又f（3）=0，则不等式
＜0的解集为（ ）
| f(x)-f(-x) |
| x |
| A、（-3，0）∪（3，+∞） |
| B、（-3，0）∪（0，3） |
| C、（-∞，-3）∪（3，+∞） |
| D、（-∞，-3）∪（0，3） |