题目内容
圆心在抛物线y2=2x上,且过定点(2,0)的圆有最小面积,则该圆的方程是 .
考点:圆的标准方程
专题:直线与圆
分析:设圆心的坐标为(
,m),由题意可得,半径的平方r2=
-m2+4 有最小值,求得半径的平方r2 取得最小值时m的值,可得此时圆的方程.
| m2 |
| 2 |
| m4 |
| 4 |
解答:
解:设圆心的坐标为(
,m),则圆的半径的平方r2=(
-2)2+(m-0)2.
由于圆的面积有最小值,∴半径的平方r2=(
-2)2+(m-0)2=
-m2+4 有最小值,
故当m2=-
=2时,半径的平方r2 取得最小值,此时,m=±
,半径的平方r2=3,
故此时,圆心的坐标为(2,±
),圆的方程为(x-1)2+(y±
)2=3,
故答案为:(x-1)2+(y±
)2=3.
| m2 |
| 2 |
| m2 |
| 2 |
由于圆的面积有最小值,∴半径的平方r2=(
| m2 |
| 2 |
| m4 |
| 4 |
故当m2=-
| -1 | ||
|
| 2 |
故此时,圆心的坐标为(2,±
| 2 |
| 2 |
故答案为:(x-1)2+(y±
| 2 |
点评:本题主要考查求圆的标准方程,二次函数的性质,求出圆心的坐标,是解题的关键,属于基础题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
如图程序框图的输出结果为6,那么判断框①表示的“条件”应该是( )


| A、i>7? | B、i>6? |
| C、i>5? | D、i>4? |
已知数列{an}满足a1=2,an+1=
,则a2014等于( )
| 1+an |
| 1-an |
| A、2 | ||
| B、-3 | ||
C、-
| ||
D、
|
若sina•
-cosa•
=-1,且a≠
﹙k∈z﹚,则a所在的象限是( )
| (sin2a) |
| (cos2a) |
| kπ |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
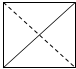 在空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,0),(1,0,1),(1,1,0),(0,1,1),且该四面体的俯视图如图,则左视图为( )
在空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,0),(1,0,1),(1,1,0),(0,1,1),且该四面体的俯视图如图,则左视图为( )