题目内容
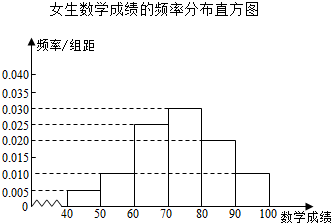
4.某校为了解高一学生的数学水平,随机抽取了高一男,女生各40人参加数学等级考试,得到男生数学成绩的频数分布表和女生数学成绩的频率分布直方图如下:男生数学成绩的频数分布表
| 成绩分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 8 | 16 | 10 | 4 |
(Ⅰ)画出男生数学成绩的频率分布直方图,并比较该校高一男,女生数学成绩的方差大小;(只需写出结论)
(Ⅱ)根据女生数学成绩的频率分布直方图,估计该校高一女生的数学平均成绩;
(Ⅲ)依据学生的数学成绩,将学生的数学水平划分为三个等级:
| 数学成绩 | 低于70分 | 70~90分 | 不低于90分 |
| 数学水平 | 一般 | 良好 | 优秀 |
分析 (Ⅰ)由男生数学成绩的频数分布表能作出男生数学成绩的频率分布直方图,由频率分布直方图得高一男生数学成绩的方差小于女生数学成绩的方差.
(Ⅱ)利用频率分布直方能求出高一女生的数学平均成绩.
(Ⅲ)由频率分布直方图能求出“高一男生数学水平良好”的概率和“高一女生数学水平良好”的概率,从而得到该校高一男生的数学水平良好的可能性大.
解答 解:(Ⅰ)∵男生数学成绩的频数分布表:
| 成绩分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 8 | 16 | 10 | 4 |

由频率分布直方图得高一男生数学成绩的方差小于女生数学成绩的方差.
(Ⅱ)高一女生的数学平均成绩为:
45×0.05+55×0.1+65×0.25+75×0.3+85×0.2+95×0.1=73.
(Ⅲ)若把频率看作相应的概率,
则“高一男生数学水平良好”的概率为:0.040×10+0.025×10=0.65,
“高一女生数学水平良好”的概率为:0.030×10+0.020×10=0.5,
所以该校高一男生的数学水平良好的可能性大.
点评 本题考查频率分布直方图的作法及应用,是基础题,解题时要认真审题,注意利用频率分布直方图求概率、平均数的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设m,n∈(0,+∞),若直线(m+2)x+(n+2)y-4=0与圆(x-1)2+(y-1)2=1相切,则m+n的最小值是( )
| A. | 4+4$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 4+$\sqrt{2}$ | D. | 4+2$\sqrt{2}$ |
19.已知函数f(x)=lnx+2sinα(α∈(0,$\frac{π}{2}$))的导函数f′(x),若存在x0<1使得f′(x0)=f(x0)成立,则实数α的取值范围为( )
| A. | ($\frac{π}{3}$,$\frac{π}{2}$) | B. | (0,$\frac{π}{3}$) | C. | ($\frac{π}{6}$,$\frac{π}{2}$) | D. | (0,$\frac{π}{6}$) |
13.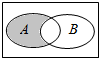 已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
 已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )| A. | {2,3,4} | B. | {2,3,4,5} | C. | {3,4} | D. | {3,4,5} |

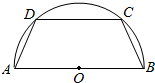 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.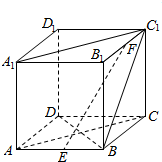 已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.
已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.