题目内容
18．某棱锥的三视图如图所示，则该几何体的体积为（ ）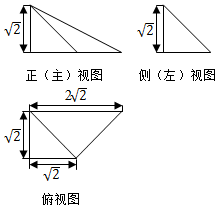
| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | 3$\sqrt{2}$ |
分析 已知中的三视图可得：该几何体是一个以俯视图为底面的四棱锥，代入锥体体积公式，可得答案．
解答 解：已知中的三视图可得：该几何体是一个以俯视图为底面的四棱锥，
其底面面积S=$\frac{1}{2}×（\sqrt{2}+3\sqrt{2}）×\sqrt{2}$=3，
高h=$\sqrt{2}$，
故体积V=$\frac{1}{3}Sh$=$\sqrt{2}$，
故选：C
点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．
练习册系列答案
相关题目
8．已知函数f（x）=x+tanx+1，若f（a）=2，则f（-a）的值为（ ）
| A． | 0 | B． | -1 | C． | -2 | D． | 3 |
9．
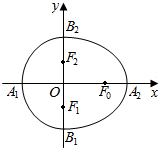我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（x＞0）与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1（x＜0）合成的曲线称作“果圆”（其中a2=b2+c2，a＞b＞c＞0）．如图，设点F0，F1，F2是相应椭圆的焦点，A1、A2和B1、B2是“果圆”与x，y轴的交点，若△F0F1F2是腰长为1的等腰直角三角形，则a，b的值分别为（ ）
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（x＞0）与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1（x＜0）合成的曲线称作“果圆”（其中a2=b2+c2，a＞b＞c＞0）．如图，设点F0，F1，F2是相应椭圆的焦点，A1、A2和B1、B2是“果圆”与x，y轴的交点，若△F0F1F2是腰长为1的等腰直角三角形，则a，b的值分别为（ ）| A． | 5，4 | B． | $\frac{{\sqrt{7}}}{2}，1$ | C． | $1，\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{6}}}{2}，1$ |
7．抛物线y=$\frac{x^2}{4}$的焦点为F，点P在抛物线上，点O为坐标原点，若|PF|=5，则|PO|等于（ ）
| A． | 6 | B． | 5$\sqrt{2}$ | C． | 5 | D． | 4$\sqrt{2}$ |
