题目内容
3.当x>0时,x2+mx+1≥0恒成立,且关于t的不等式t2+2t+m≤0有解,则实数m的取值范围是( )| A. | [1,+∞) | B. | [-2,1] | C. | (-∞,-2]∪[1,+∞) | D. | (-∞,-2] |
分析 由当x>0时,x2+mx+1≥0恒成立,得到m≥-(x+$\frac{1}{x}$),利用基本不等式即可求出m的范围,再根据关于t的不等式t2+2t+m≤0有解,则△=4-4m≥0,最后求其交集即可.
解答 解:∵当x>0时,x2+mx+1≥0恒成立,
∴m≥-(x+$\frac{1}{x}$),
∵x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,当且仅当x=1时取等号,
∴m≥-2,
∵关于t的不等式t2+2t+m≤0有解,
∴△=4-4m≥0,
∴m≤1,
∴实数m的取值范围是[-2,1],
故选:B.
点评 本题考查的知识点是二次函数的图象和性质以及基本不等式,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
11.已知命题p:?x0∈R,x02<x0,命题q:?x∈R,x2-x+1>0,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
12.三棱锥A-BCD中,AB=AC=AD=2,∠BAD=90°,∠BAC=60°,则$\overrightarrow{AB}$•$\overrightarrow{CD}$等于( )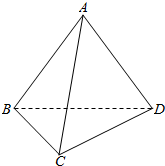

| A. | -2 | B. | 2 | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
