题目内容
3.设正项等差数列{an}的前n项和为Sn,若S2017=4034,则$\frac{1}{a_9}+\frac{9}{{{a_{2009}}}}$的最小值为( )| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | 4 |
分析 由差数列的前n项和公式,求出a1+a2017=4.由等差数列的性质得a9+a2009=4,由此利用基本不等式能求出$\frac{1}{a_2}+\frac{1}{{{a_{2008}}}}$的最小值.
解答 解:由差数列的前n项和公式,得${S_{2017}}=\frac{{2017({a_1}+{a_{2017}})}}{2}=4034$,
则a1+a2017=4.
由等差数列的性质得a9+a2009=4,
∴$\frac{1}{a_9}+\frac{9}{{{a_{2009}}}}=\frac{1}{4}({a_9}+{a_{2009}})(\frac{1}{a_9}+\frac{9}{{{a_{2009}}}})=\frac{1}{4}(10+\frac{{{a_{2009}}}}{a_9}+\frac{{9{a_9}}}{{{a_{2009}}}})≥\frac{1}{4}(10+2\sqrt{\frac{{{a_{2009}}}}{a_9}×\frac{{9{a_9}}}{{{a_{2009}}}}})=\frac{1}{4}(10+6)=4$.
故选:D.
点评 本题考查数列两项倒数和的最小值的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知函数f(x)=log2(x2-ax+3a),对于任意x≥2,当△x>0时,恒有f(x+△x)>f(x),则实数a的取值范围是( )
| A. | (-∞,4) | B. | (-4,4] | C. | (-∞,-4)∪[2,+∞) | D. | [-4,2) |
11.已知复数z满足(1-i)z=i,则复数$\overline{z}$在复平面内的对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.已知复数$z=\frac{5}{2i-1}$(i为虚数单位),则z的共轭复数对应的点位于复平面的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.“α=$\frac{π}{6}$”是$tan({π-a})=-\frac{{\sqrt{3}}}{3}$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
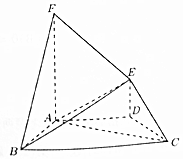 在如图所示的多面体中,DE⊥平面ABCD,AF∥DE,AD∥BC,AB=CD,∠ABC=60°,BC=2AD=4DE=4.
在如图所示的多面体中,DE⊥平面ABCD,AF∥DE,AD∥BC,AB=CD,∠ABC=60°,BC=2AD=4DE=4.