题目内容
设集合A={x|-2≤x≤5},
(1).设U=R,若B={x|m≤x≤m+3},且(∁UA)∩B=∅,求实数m的取值范围;
(2).若B={x|m+1≤x≤2m-1},且A∪B=A,求实数m的取值范围.
(1).设U=R,若B={x|m≤x≤m+3},且(∁UA)∩B=∅,求实数m的取值范围;
(2).若B={x|m+1≤x≤2m-1},且A∪B=A,求实数m的取值范围.
考点:并集及其运算,交、并、补集的混合运算
专题:集合
分析:(1)由集合A及全集求出CUA,再由(∁UA)∩B=∅得到两集合端点值见得关系,解不等式组得答案;
(2)由A∪B=A得B⊆A,然后分B=∅和B≠∅分类求解m的范围,取并集后得答案.
(2)由A∪B=A得B⊆A,然后分B=∅和B≠∅分类求解m的范围,取并集后得答案.
解答:
解:(1)由已知得:CUA={x|x<-2或x>5},
∵(∁UA)∩B=∅,
∴
,解得:-2≤m≤2.
∴m的取值范围是:{m|-2≤m≤2};
(2)若A∪B=A,则B⊆A,
①当B=∅时,则m+1>2m-1,解得m<2,满足B⊆A.
②当B≠∅时,要使B⊆A成立,则:
,解得:2≤m≤3.
综上所述,m的取值范围是:{m|m≤3}.
∵(∁UA)∩B=∅,
∴
|
∴m的取值范围是:{m|-2≤m≤2};
(2)若A∪B=A,则B⊆A,
①当B=∅时,则m+1>2m-1,解得m<2,满足B⊆A.
②当B≠∅时,要使B⊆A成立,则:
|
综上所述,m的取值范围是:{m|m≤3}.
点评:本题考查了交、并、补集的混合运算,考查了分类讨论的解题方法,是中档题.

练习册系列答案
相关题目
下列是映射的是( )


| A、1、2、3 | B、1、2 |
| C、1、3 | D、2、3 |
函数y=
的定义域为( )
| log2(2x2-x) |
A、{x|x≤-
| ||
B、{x|x<-
| ||
C、{x|x≤0,或x≥
| ||
D、{x|x<0,或x>
|
若直线l:y=kx-
与直线x+y-3=0的交点位于第二象限,则直线l的倾斜角的取值范围是( )
| 3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
设集合M={x∈Z|x2+2x≤0},N={x|x2-2x=0,x∈R},则M∩N=( )
| A、{0} |
| B、{0,2} |
| C、{-2,0} |
| D、{-2,0,2} |
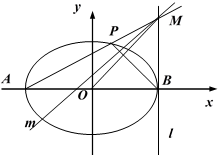 (1)求椭圆E的方程;
(1)求椭圆E的方程;