题目内容
若直线l：y=kx-
与直线x+y-3=0的交点位于第二象限，则直线l的倾斜角的取值范围是（ ）
| 3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、（
|
考点：其他不等式的解法,两条直线的交点坐标
专题：不等式的解法及应用
分析：求出直线的交点坐标，利用交点位于第二象限，求解k的范围，然后求解直线l的倾斜角的取值范围．
解答：
解：联立两直线方程得：
，
解得：x=
，y=
，
所以两直线的交点坐标为（
，
），
因为两直线的交点在第二象限，所以得到
，
解得：k＜-1，
设直线l的倾斜角为θ，则tanθ＜-1，所以θ∈(
，
)．
故选：B．
|
解得：x=
3+
| ||
| 1+k |
3k-
| ||
| 1+k |
所以两直线的交点坐标为（
3+
| ||
| 1+k |
3k-
| ||
| 1+k |
因为两直线的交点在第二象限，所以得到
|
解得：k＜-1，
设直线l的倾斜角为θ，则tanθ＜-1，所以θ∈(
| π |
| 2 |
| 3π |
| 4 |
故选：B．
点评：此题考查学生会根据两直线的方程求出交点的坐标，掌握象限点坐标的特点，掌握直线倾斜角与直线斜率的关系，是一道综合题．
练习册系列答案
相关题目
若复数z1=5+5i，z2=3-i，则
=（ ）
| z1 |
| z2 |
| A、4+2i | B、2+i |
| C、1+2i | D、3 |
命题p：?x∈[0，+∞），（log32）x≤1，则下列说法正确的是（ ）
| A、p是假命题：￢p：?x0∈[0，+∞），（log32）x0＞1 |
| B、p是假命题：￢p：?x∈[0，+∞），（log32）x≥1 |
| C、p是真命题：￢p：?x0∈[0，+∞），（log32）x0＞1 |
| D、p是假命题：￢p：?x∈[0，+∞），（log32）x≥1 |
若全集A={-1，0，1}，则集合A的子集共有（ ）
| A、3个 | B、5个 | C、7个 | D、8个 |
设集合A={x|-2≤x≤5}，
（1）．设U=R，若B={x|m≤x≤m+3}，且（∁UA）∩B=∅，求实数m的取值范围；
（2）．若B={x|m+1≤x≤2m-1}，且A∪B=A，求实数m的取值范围．
（1）．设U=R，若B={x|m≤x≤m+3}，且（∁UA）∩B=∅，求实数m的取值范围；
（2）．若B={x|m+1≤x≤2m-1}，且A∪B=A，求实数m的取值范围．
命题“?x0∈Q，sinx0+cosx0-2 Φ0≤0”的否定是（ ）
| A、?x0∉Q，sinx0+cosx0-2 Φ0≤0 |
| B、?x0∈Q，sinx0+cosx0-2 Φ0＞0 |
| C、?x∈Q，sinx+cosx-2Φ≤0 |
| D、?x∈Q，sinx+cosx-2Φ＞0 |
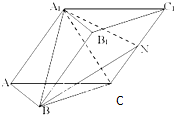己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形，侧面A1ACC1为菱形，∠A1AC=60°，平面A1ACC1⊥平面ABC，N是CC1的中点．