题目内容
8.已知过点M(2,0)的动直线l交抛物线y2=2x于A,B两点,则$\overrightarrow{OA}$•$\overrightarrow{OB}$的值为( )| A. | 2 | B. | 0 | C. | 4 | D. | -2 |
分析 设出过点M的直线方程,和抛物线方程联立后利用根与系数关系得到A,B两点的横纵坐标的积,代入数量积的坐标公式得答案.
解答 解:设过点M(2,0)的直线l的方程为:x=ty+2,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{x=ty+2}\\{{y}^{2}=2x}\end{array}\right.$
得:y2-2ty-4=0.
∴y1+y2=2t,y1y2=-4.
x1x2=(ty1+2)(ty2+2)=t2y1y2+2t(y1+y2)+4=-2t2+2t2+4=4.
则$\overrightarrow{OA}$•$\overrightarrow{OB}$的=x1x2+y1y2=4-4=0.
故选:B.
点评 本题考查了直线与圆锥曲线的关系,考查了平面向量的数量积运算,涉及直线与圆锥曲线的关系问题,常采用联立方程组,化为关于x的方程后利用一元二次方程根与系数的关系解决,是中档题.

练习册系列答案
相关题目
18.已知x∈[-1,0],θ∈[0,2π),二元函数$f(x,θ)=\frac{1+cosθ+x}{1+sinθ-x}$取最小值时,x=x0,θ=θ0则( )
| A. | 4x0+θ0=0 | B. | 4x0+θ0<0 | C. | 4x0+θ0>0 | D. | 以上均有可能. |
19.已知函数f(x)=$\left\{\begin{array}{l}{sin\frac{π}{2}x-1,x<0}\\{lo{g}_{a}x,x>0}\end{array}\right.$(a>0且a≠1)的图象上关于y轴对称的点至少有3对,则实数a的范围是( )
| A. | (0,$\frac{\sqrt{5}}{5}$) | B. | ($\frac{\sqrt{5}}{5}$,1) | C. | ($\frac{\sqrt{3}}{5}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
17.已知x,y的值如表所示,如果y与x呈线性相关且回归直线方程为$\widehat{y}$=$\widehat{b}$x+2,则$\widehat{b}$=( )
| x | 2 | 3 | 4 |
| y | 5 | 4 | 6 |
| A. | 3 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
1.$\int_1^2{\frac{2}{x}}dx$=( )
| A. | 2ln2 | B. | -2ln2 | C. | ln2 | D. | -ln2 |
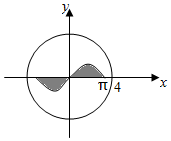 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)=$\frac{1}{2π}$.