题目内容
15.设y=f(x)在R上有定义.对于给定的正数K,定义fk(x)=$\left\{\begin{array}{l}{f(x),f(x)≤K}\\{K,f(x)>K}\end{array}\right.$,取函数f(x)=$2-x-\frac{1}{e^x}$.若对任意的x∈R,恒有fk(x)=f(x),则( )| A. | K的最小值为1 | B. | K的最小值为2 | C. | K的最大值为1 | D. | K的最大值为2 |
分析 根据新定义的函数建立fk(x)与f(x)之间的关系,通过二者相等得出实数k满足的条件,利用导数或者函数函数的单调性求解函数的最值,进而求出k的范围,进一步得出所要的结果.
解答 解:由题意可得出k≥f(x)最大值,
由于f′(x)=-1+e-x,令f′(x)=0,e-x=1=e0解出-x=0,即x=0,
当x>0时,f′(x)<0,f(x)单调递减,
当x<0时,f′(x)>0,f(x)单调递增.
故当x=0时,f(x)取到最大值f(0)=2-1=1.
故当k≥1时,恒有fk(x)=f(x).
因此K的最小值是1.
故选:A.
点评 本题考查学生对新定义型问题的理解和掌握程度,理解好新定义的分段函数是解决本题的关键,将所求解的问题转化为求解函数的最值问题,利用了导数的工具作用,体现了恒成立问题的解题思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.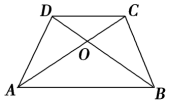 如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC:S△AOD=CD:AB;
④S△AOD=S△BOC.
其中正确的个数为( )
 如图所示,梯形ABCD的对角线交于点O,则下列四个结论:
如图所示,梯形ABCD的对角线交于点O,则下列四个结论:①△AOB∽△COD;
②△AOD∽△ACB;
③S△DOC:S△AOD=CD:AB;
④S△AOD=S△BOC.
其中正确的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.阅读如图所示的程序框图,则输出的S的值是( )


| A. | $\frac{8}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{7}{8}$ | D. | $\frac{6}{7}$ |