题目内容
已知p:b2-4ac≥0(a≠0),q:ax2+bx+c=0(a≠0)有实数根,那么p是q的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据一元二次方程有实根则判别式△≥0,若△≥0,则对应一元二次方程有实根,所以p是q的充要条件.
解答:
解:若方程ax2+bx+c=0(a≠0)有实数根,则判别式△=b2-4ac≥0;
若△=b2-4ac≥0(a≠0),则方程ax2+bx+c=0有实数根;
所以p是q的充要条件.
故选;C.
若△=b2-4ac≥0(a≠0),则方程ax2+bx+c=0有实数根;
所以p是q的充要条件.
故选;C.
点评:考查一元二次方程的根和判别式的关系,充要条件的概念.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)是R上的奇函数,且f(1)=2,f(x+3)=f(x),则f(8)=( )
| A、2 | B、-2 | C、0 | D、2或0 |
将长为8宽为4的矩形纸片卷成一个圆柱,则圆柱的最大体积为( )
| A、65π | ||
| B、32π | ||
C、
| ||
D、
|
一个算法的程序框图如图所示,若该程度输出的结果为
,则判断框①中应填入的条件是( )

| 7 |
| 12 |

| A、i<5 | B、i<4 |
| C、i>4 | D、i≤3 |
已知A={x|x2-4x+3≤0},B={x|x2+mx+n<0},且A∩B≠∅,A∪B={x|1≤x<4},则m2-
n的取值范围为( )
| 5 |
| 2 |
| A、[15,19] |
| B、[14,18] |
| C、[15,19) |
| D、[14,18) |
已知函数f(x)=Acos(ωx+φ)的图象如图所示,f(
)=-
,则f(-
)=( )

| π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |

A、-
| ||
B、
| ||
C、-
| ||
D、
|
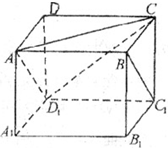 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: