题目内容
7. 如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.(1)求BD得长;
(2)求∠ABC+∠ADC的值.
分析 (1)根据正弦定理和余弦定理进行求解即可.
(2)根据余弦定理先求出∠C的大小即可得到结论.
解答 解:(1)在△ABD中,因为cos∠ADB=$\frac{1}{7}$.∠ADB∈(0,π),
所以sin∠ADB=$\frac{4\sqrt{3}}{7}$,
根据正弦定理,有$\frac{BD}{sinA}=\frac{AB}{sin∠ADB}$,
代入AB=4,∠A=$\frac{π}{3}$,解得BD=$\frac{7}{2}$; …(6分)
(2)在△BCD中,根据余弦定理cos∠C=$\frac{B{C}^{2}+C{D}^{2}-B{D}^{2}}{2BC•CD}$,代入BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,
得cos∠C=$-\frac{1}{2}$,
因为∠C∈(0,π),
所以∠C=$\frac{2π}{3}$,所以∠A+∠C=π,而在四边形ABCD中∠A+∠ABC+∠C+∠ADC=2π,
所以∠ABC+∠ADC=π …(12分)
点评 本题主要考查解三角形的应用,利用正弦定理和余弦定理是解决本题的关键.考查学生的运算和推理能力.

练习册系列答案
相关题目
17.正弦函数f(x)=sinx图象的一条对称轴是( )
| A. | x=0 | B. | $x=\frac{π}{4}$ | C. | $x=\frac{π}{2}$ | D. | x=π |
18. 已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )
已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )
 已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )
已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )| A. | x1>x2,s12<s22 | B. | x1=x2,s12>s22 | C. | x1=x2,s12=s22 | D. | x1=x2,s12<s22 |
15.在长方体ABCD-A1B1C1D1中,$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{D{D_1}}$=( )
| A. | $\overrightarrow{{D_1}{B_1}}$ | B. | $\overrightarrow{{D_1}B}$ | C. | $\overrightarrow{D{B_1}}$ | D. | $\overrightarrow{B{D_1}}$ |
2.设f(x)是定义域为R且最小正周期为2π的函数,且有f(x)=$\left\{\begin{array}{l}{sinx,0≤x≤π}\\{cosx,-π<x<0}\end{array}\right.$,则f(-$\frac{13π}{4}$)=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | 0 | D. | 1 |
12.命题“若x>2,则x2+x>6”的逆否命题是( )
| A. | 若x>2,则x2+x≤6 | B. | 若x2+x≤6,则x≤2 | C. | 若x2+x<6,则x<2 | D. | 若x≤2,则x2+x≤6 |
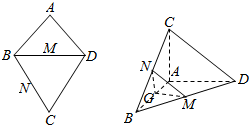 如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.
如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.