题目内容
12.已知0<α<$\frac{π}{2}$,3sin(π-α)=-2cos(π+α).(1)求$\frac{4sinα-2cosα}{5cosα+3sinα}$的值;
(2)求$cos2α+sin(α+\frac{π}{2})$的值.
分析 由已知求得tanα的值.
(1)化弦为切可求$\frac{4sinα-2cosα}{5cosα+3sinα}$的值;
(2)由tanα的值,再由同角三角函数的基本关系式求得cosα,则$cos2α+sin(α+\frac{π}{2})$的值可求.
解答 解:由3sin(π-α)=-2cos(π+α),得3sinα=2cosα,
∴tanα=$\frac{2}{3}$.
(1)$\frac{4sinα-2cosα}{5cosα+3sinα}$=$\frac{4tanα-2}{5+3tanα}=\frac{4×\frac{2}{3}-2}{5+3×\frac{2}{3}}=\frac{2}{21}$;
(2)∵tanα=$\frac{2}{3}$,∴$secα=\sqrt{1+ta{n}^{2}α}=\frac{\sqrt{13}}{3}$,则cosα=$\frac{3\sqrt{13}}{13}$.
∴$cos2α+sin(α+\frac{π}{2})$=cos2α+cosα=2cos2α+cosα-1=$2×(\frac{3\sqrt{13}}{13})^{2}+\frac{3\sqrt{13}}{13}-1$=$\frac{5+3\sqrt{13}}{13}$.
点评 本题考查三角函数的化简求值,考查同角三角函数基本关系式的应用,是基础的计算题.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
7.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2sinx,则当x<0时,f(x)=( )
| A. | -x2-2sinx | B. | -x2+2sinx | C. | x2+2sinx | D. | x2-2sinx |
4.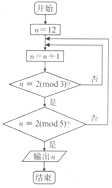 若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )
若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )
 若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )
若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
1.运行如图所示的程序框图,输出的结果S=( )


| A. | 14 | B. | 30 | C. | 62 | D. | 126 |
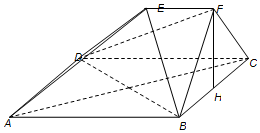 如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,