题目内容
7．已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-2sinx，则当x＜0时，f（x）=（ ）| A． | -x2-2sinx | B． | -x2+2sinx | C． | x2+2sinx | D． | x2-2sinx |
分析 函数f（x）是定义在R上的奇函数，可得f（-x）=-f（x），当x≥0时，f（x）=x2-2sinx，当x＜0时，-x＞0，带入化简可得x＜0时f（x）的解析式．
解答 解：函数f（x）是定义在R上的奇函数，
∴f（-x）=-f（x），
当x≥0时，f（x）=x2-2sinx，
当x＜0时，则-x＞0，可得f（-x）=x2+2sinx=-f（x），
∴f（x）=-x2-2sinx，
故选：A．
点评 本题考查了函数解析式的求法，利用了函数的奇偶性，转化的思想，属于基础题．
练习册系列答案
相关题目
17．已知函数f（x）=2sin（ωx+φ）+1（ω＞0，|φ|≤$\frac{π}{2}}$），其图象与直线y=2最近的两个相邻交点间的距离为$\frac{π}{3}$，若f（x）＞1对$?x∈（{-\frac{π}{8}，\frac{π}{3}}）$恒成立，则φ的取值范围是（ ）
| A． | $[{\frac{π}{4}，\frac{π}{3}}]$ | B． | $[{-\frac{π}{6}，\frac{π}{4}}]$ | C． | $[{\frac{π}{6}，\frac{π}{4}}]$ | D． | $（{\frac{π}{6}，\frac{π}{2}}]$ |
15．将一枚均匀硬币先后抛两次，恰好有一次出现正面的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
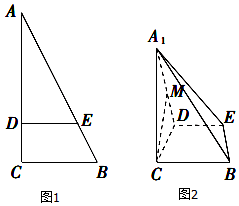如图，在△ABC中，∠C=90°，BC=3，AC=6，D，E分别是AC，AB上的点，且DE∥BC，DE=2．将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD．
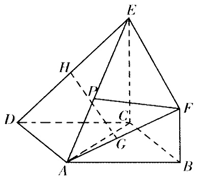在如图所示的空间几何体中，EC⊥平面ABCD，四边形ABCD是菱形，CE∥BF，且CE=2BF，G，H，P分别为AF，DE，AE的中点．求证：
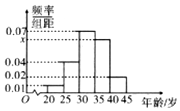为创建全国文明城市，某区向各事业行政单位征集“文明过马路”义务督导员．从符合条件的600名志愿者中随机抽取100名，按年龄作分组如下：[20，25），[25，30），[30，35），[35，40），[40，45]，并得到如下频率分布直方图．