题目内容
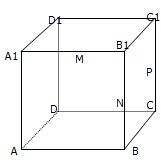 如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.
如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.(1)证明D1M、C1B1、CN三线共点;
(2)求异面直线D1P与AM所成角度数并求CN与AM所成角的余弦值.
考点:异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)先说明D1M∩CN=K,再说明K∈B1C1,从而D1M、C1B1、CN三线共点;
(2)利用平行线作出异面直线所成的角,再在三角形中计算.
(2)利用平行线作出异面直线所成的角,再在三角形中计算.
解答:
(1)证明:M、N分别为A1B1、BB1的中点,∴MN∥A1B,MN=
A1B,∴MN∥D1C,∴M、N、D1、C共面,D1M∩CN=K,D1、M∈面,C、N∈面BC1,面A1C1∩面BC1=B1C1,∴K∈B1C1,D1M、C1B1、CN三线共点; 
(2)解:连接A1N,由题意,A1N∥D1P,异面直线D1P与AM所成角即A1N与AM所成角,由题意,Rt△AA1M≌Rt△A1B1N,∴∠A1MA=∠B1NA1
Rt△A1B1N中,∠B1NA1+∠B1A1N=90°,∴∠A1MA+∠B1A1N=90°,即∠A1FM=90°,∴异面直线D1P与AM所成角度数90°;
G为AB中点,E为BG中点,EN∥AM,∠CNE即CN与AM所成角,在△CNE中,NE=
,CN=
,CE=
,cos∠CNE=
=
| 1 |
| 2 |

(2)解:连接A1N,由题意,A1N∥D1P,异面直线D1P与AM所成角即A1N与AM所成角,由题意,Rt△AA1M≌Rt△A1B1N,∴∠A1MA=∠B1NA1
Rt△A1B1N中,∠B1NA1+∠B1A1N=90°,∴∠A1MA+∠B1A1N=90°,即∠A1FM=90°,∴异面直线D1P与AM所成角度数90°;
G为AB中点,E为BG中点,EN∥AM,∠CNE即CN与AM所成角,在△CNE中,NE=
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| NE2+NC2-CE2 |
| 2NE•NC |
| 2 |
| 5 |
点评:课题考查三线共点,及异面直线所成的角,相关定理、概念的熟练掌握是关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
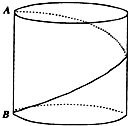 如图,底面半径为1,高为2的圆柱,有A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?
如图,底面半径为1,高为2的圆柱,有A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少? 如图,已知AB为圆O的一条直径,以端点B为圆心的圆交直线AB于C、D两点,交圆O于E、F两点,过点D作垂直于AD的直线,交直线AF于H点.
如图,已知AB为圆O的一条直径,以端点B为圆心的圆交直线AB于C、D两点,交圆O于E、F两点,过点D作垂直于AD的直线,交直线AF于H点. 如图所示,等腰△ABC的底边AB=6
如图所示,等腰△ABC的底边AB=6 如图,在直三棱柱ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点,且B1M与平面ACC1所成角为30°.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点,且B1M与平面ACC1所成角为30°.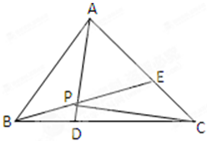 如图,在正△ABC中,点D、E分别在边BC,AC上,且BD=
如图,在正△ABC中,点D、E分别在边BC,AC上,且BD=