题目内容
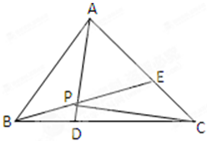 如图,在正△ABC中,点D、E分别在边BC,AC上,且BD=
如图,在正△ABC中,点D、E分别在边BC,AC上,且BD=| 1 |
| 3 |
| 1 |
| 3 |
(Ⅰ)四点P、D、C、E共圆;
(Ⅱ)AP⊥CP.
考点:圆內接多边形的性质与判定
专题:直线与圆
分析:(I)由已知条件推导出△ABD≌△BCE,由此能证明四点P,D,C,E共圆.
(II)连结DE,由正弦定理知∠CED=90°,由四点P,D,C,E共圆知,∠DPC=∠DEC,由此能证明AP⊥CP.
(II)连结DE,由正弦定理知∠CED=90°,由四点P,D,C,E共圆知,∠DPC=∠DEC,由此能证明AP⊥CP.
解答:
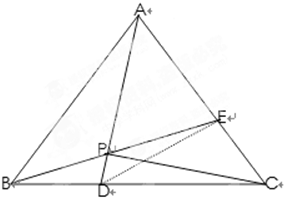 证明:(I)在△ABC中,由BD=
证明:(I)在△ABC中,由BD=
BC,CE=
CA,知:
△ABD≌△BCE,…(2分)
∴∠ADB=∠BEC,即∠ADC+∠BEC=π.
所以四点P,D,C,E共圆.…(5分)
(II)如图,连结DE.
在△CDE中,CD=2CE,∠ACD=60°,
由正弦定理知∠CED=90°.…(8分)
由四点P,D,C,E共圆知,∠DPC=∠DEC,
所以AP⊥CP.…(10分)
 证明:(I)在△ABC中,由BD=
证明:(I)在△ABC中,由BD=| 1 |
| 3 |
| 1 |
| 3 |
△ABD≌△BCE,…(2分)
∴∠ADB=∠BEC,即∠ADC+∠BEC=π.
所以四点P,D,C,E共圆.…(5分)
(II)如图,连结DE.
在△CDE中,CD=2CE,∠ACD=60°,
由正弦定理知∠CED=90°.…(8分)
由四点P,D,C,E共圆知,∠DPC=∠DEC,
所以AP⊥CP.…(10分)
点评:本题考查四点共圆的证明,考查异面直线垂直的证明,解题时要认真审题,注意正弦定理的合理运用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
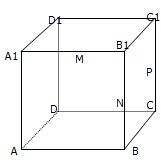 如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.
如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.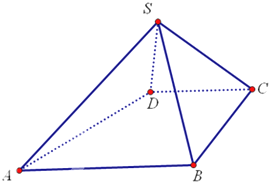 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.