题目内容
 如图,已知AB为圆O的一条直径,以端点B为圆心的圆交直线AB于C、D两点,交圆O于E、F两点,过点D作垂直于AD的直线,交直线AF于H点.
如图,已知AB为圆O的一条直径,以端点B为圆心的圆交直线AB于C、D两点,交圆O于E、F两点,过点D作垂直于AD的直线,交直线AF于H点.(Ⅰ)求证:B、D、H、F四点共圆;
(Ⅱ)若AC=2,AF=2
| 2 |
考点:圆內接多边形的性质与判定,与圆有关的比例线段
专题:直线与圆
分析:(Ⅰ)由已知条件推导出BF⊥FH,DH⊥BD,由此能证明B、D、F、H四点共圆.
(2)因为AH与圆B相切于点F,由切割线定理得AF2=AC•AD,解得AD=4,BF=BD=1,由△AFB∽△ADH,得DH=
,由此能求出△BDF的外接圆半径.
(2)因为AH与圆B相切于点F,由切割线定理得AF2=AC•AD,解得AD=4,BF=BD=1,由△AFB∽△ADH,得DH=
| 2 |
解答:
(Ⅰ)证明:因为AB为圆O一条直径,所以BF⊥FH,…(2分)
 又DH⊥BD,
又DH⊥BD,
故B、D、F、H四点在以BH为直径的圆上,
所以B、D、F、H四点共圆.…(4分)
(2)解:因为AH与圆B相切于点F,
由切割线定理得AF2=AC•AD,即(2
)2=2•AD,
解得AD=4,…(6分)
所以BD=
(AD-AC)=1,BF=BD=1,
又△AFB∽△ADH,
则
=
,得DH=
,…(8分)
连接BH,由(1)知BH为DBDF的外接圆直径,
BH=
=
,
故△BDF的外接圆半径为
.…(10分)
 又DH⊥BD,
又DH⊥BD,故B、D、F、H四点在以BH为直径的圆上,
所以B、D、F、H四点共圆.…(4分)
(2)解:因为AH与圆B相切于点F,
由切割线定理得AF2=AC•AD,即(2
| 2 |
解得AD=4,…(6分)
所以BD=
| 1 |
| 2 |
又△AFB∽△ADH,
则
| DH |
| BF |
| AD |
| AF |
| 2 |
连接BH,由(1)知BH为DBDF的外接圆直径,
BH=
| BD2+DH2 |
| 3 |
故△BDF的外接圆半径为
| ||
| 2 |
点评:本题考查四点共圆的证明,考查三角形处接圆半径的求法,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).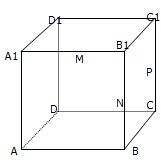 如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.
如图,在棱长为1的正方形ABCD-A1B1C1D1中,M、N、P分别为A1B1、BB1、CC1的中点.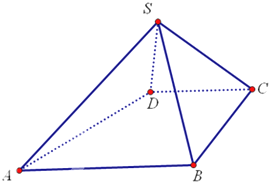 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.