��Ŀ����
6����֪����M={��x��y��|y=f��x��}�����������⣨x1��y1����M�����ڣ�x2��y2����M��ʹ��x1x2+y1y2=0��������Ƽ���M�ǡ������ϡ�����������4�����ϣ���M={��x��y��|y=lgx} ���� ������
��M={��x��y��|y=cosx+sinx}
��M={��x��y��|y=-$\frac{1}{x}$} �������� ����
��M={��x��y��|y=ex-3}
�����ǡ������ϡ�����������ǣ�������
| A�� | �ڢ� | B�� | �ڢ� | C�� | �٢ڢ� | D�� | �٢ۢ� |
���� �۲�ѡ������ų���ȷ���𰸣�
��� �⣺��֪��1��0����M���������ڣ�0��y����M���ʢٲ���ȷ��
���ų�C��D��
�裨x1��y1����M����x2��y2����M��
��x1x2+��-$\frac{1}{{x}_{1}}$����-$\frac{1}{{x}_{2}}$��=x1x2+$\frac{1}{{x}_{1}}$$\frac{1}{{x}_{2}}$��
�ɻ�������ʽ֪��|x1x2+$\frac{1}{{x}_{1}}$$\frac{1}{{x}_{2}}$|��2��
�ʢ۲���ȷ��
���ų�A��
��ѡB��
���� ���⿼���˼����뺯��������ʽ�������ų����Ƚϼ�

��ϰ��ϵ�д�
�����Ŀ
16����֪˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$�����ҽ���ֱ�ΪF1��F2����F2��ֱ�߽�˫������P��Q������PQ��PF1����|PQ|=��|PF1|��$\frac{5}{12}�ܦˡ�\frac{4}{3}$����˫����������e��ȡֵ��ΧΪ��������
| A�� | $��1��\frac{{\sqrt{10}}}{2}]$ | B�� | $��1��\frac{{\sqrt{37}}}{5}]$ | C�� | $[\frac{{\sqrt{37}}}{5}��\frac{{\sqrt{10}}}{2}]$ | D�� | $[\frac{{\sqrt{10}}}{2}��+�ޣ�$ |
17����������[0����]�����ȡһ����x����sinx��ֵ�������䣨$\frac{1}{2}$��1���ڵĸ���Ϊ��������
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{2}{��}$ |
14��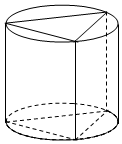 ��ͼ��Բ������һ�����������������ĵ�����Բ�������ڣ��ҵ������������Σ�Բ�������Ϊ16�У������ֱ����ĸ�߳���ȣ���������������Ϊ��������
��ͼ��Բ������һ�����������������ĵ�����Բ�������ڣ��ҵ������������Σ�Բ�������Ϊ16�У������ֱ����ĸ�߳���ȣ���������������Ϊ��������
 ��ͼ��Բ������һ�����������������ĵ�����Բ�������ڣ��ҵ������������Σ�Բ�������Ϊ16�У������ֱ����ĸ�߳���ȣ���������������Ϊ��������
��ͼ��Բ������һ�����������������ĵ�����Բ�������ڣ��ҵ������������Σ�Բ�������Ϊ16�У������ֱ����ĸ�߳���ȣ���������������Ϊ��������| A�� | 6$\sqrt{3}$ | B�� | 12 | C�� | 12$\sqrt{3}$ | D�� | 16$\sqrt{3}$ |
18�����к����У����䶨�����ڼ����溯�����ǵ��������ĺ����ǣ�������
| A�� | y=-$\frac{1}{x}$ | B�� | y=3-x-3x | C�� | y=x|x| | D�� | y=x3-x |
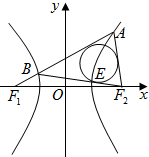 ��֪F1��F2��˫����C��$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1��a��0��b��0�������ҽ��㣬|F1F2|=4����A��˫���ߵ���֧�ϣ��߶�AF1��˫������֧�ཻ�ڵ�B����F2AB������Բ���BF2�����ڵ�E����|AF2|=2|BF1|��|BE|=2$\sqrt{2}$����˫����C��������Ϊ$\sqrt{2}$��
��֪F1��F2��˫����C��$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1��a��0��b��0�������ҽ��㣬|F1F2|=4����A��˫���ߵ���֧�ϣ��߶�AF1��˫������֧�ཻ�ڵ�B����F2AB������Բ���BF2�����ڵ�E����|AF2|=2|BF1|��|BE|=2$\sqrt{2}$����˫����C��������Ϊ$\sqrt{2}$��