题目内容
1.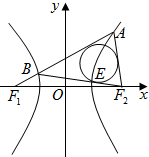 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,|F1F2|=4,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与边BF2相切于点E.若|AF2|=2|BF1|,|BE|=2$\sqrt{2}$,则双曲线C的离心率为$\sqrt{2}$.
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,|F1F2|=4,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与边BF2相切于点E.若|AF2|=2|BF1|,|BE|=2$\sqrt{2}$,则双曲线C的离心率为$\sqrt{2}$.
分析 设|BF1|=m,则|AF2|=2m,由双曲线的定义可得|AF1|=2a+2m,|BF2|=m+2a,|EF2|=m+2a-2$\sqrt{2}$,再由内切圆的性质,求得a=$\sqrt{2}$,结合离心率公式,可得所求.
解答 解:设|BF1|=m,则|AF2|=2m,
由双曲线的定义有|AF1|=|AF2|+2a=2a+2m,
|BF2|=m+2a,|EF2|=m+2a-2$\sqrt{2}$,
即有2a+2m=2m-(m+2a-2$\sqrt{2}$)+2$\sqrt{2}$+m,
解得a=$\sqrt{2}$,
由c=2,可得e=$\frac{c}{a}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查双曲线的定义、方程和性质,考查内切圆的性质,考查离心率的求法,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
11.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为e,一条渐近线的方程为y=$\sqrt{2e-1}$x,则e=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
12.已知过定点P(2,0)的直线l与曲线$y=\sqrt{2-{x^2}}$相交于A,B两点,O为坐标原点,当△AOB的面积最大时,直线l的倾斜角为( )
| A. | 150° | B. | 135° | C. | 120° | D. | 30° |
9.已知等差数列{an}满足an∈N*,且前10项和S10=280,则a9的最大值为( )
| A. | 29 | B. | 49 | C. | 50 | D. | 58 |
11.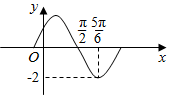 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f($\frac{19π}{6}$)的值为( )
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f($\frac{19π}{6}$)的值为( )
 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f($\frac{19π}{6}$)的值为( )
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f($\frac{19π}{6}$)的值为( )| A. | 0 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |