题目内容
7.定义在R上的函数y=f(x)为减函数,且函数y=f(x-1)的图象关于点(1,0)对称,若f(x2-2x)+f(2b-b2)≤0,且0≤x≤2,则x-b的取值范围是[-2,2].分析 根据题意,分析可得函数f(x)为奇函数,则可以将f(x2-2x)+f(2b-b2)≤0转化为f(x2-2x)<f(b2-2b),结合函数的单调性进一步可以转化为|x-1|≥|b-1|,即可得
$\left\{\begin{array}{l}{0≤x≤1}\\{x≤b≤2-x}\end{array}\right.$或$\left\{\begin{array}{l}{1≤x≤2}\\{2-x≤b≤x}\end{array}\right.$,建立如图的坐标系:设z=x-b,借助线性规划的性质分析可得x-b的最大、最小值,即可得答案.
解答  解:根据题意,函数y=f(x-1)的图象关于点(1,0)对称,则函数f(x)的图象关于原点(0,0)对称,即函数f(x)为奇函数;
解:根据题意,函数y=f(x-1)的图象关于点(1,0)对称,则函数f(x)的图象关于原点(0,0)对称,即函数f(x)为奇函数;
f(x2-2x)+f(2b-b2)≤0?f(x2-2x)<-f(2b-b2)?f(x2-2x)<f(b2-2b),
又由函数f(x)为减函数,则f(x2-2x)<f(b2-2b)?x2-2x>b2-2b?|x-1|≥|b-1|,
又由0≤x≤2,则有$\left\{\begin{array}{l}{0≤x≤1}\\{x≤b≤2-x}\end{array}\right.$或$\left\{\begin{array}{l}{1≤x≤2}\\{2-x≤b≤x}\end{array}\right.$,
建立如图的坐标系:设z=x-b,
分析可得对于直线b=x-z,当其过点(2,0)时,Z有最大值2,当其过点(0,2)时,Z有最小值-2,
故x-b的取值范围[-2,2];
故答案为:[-2,2].
点评 本题考查线性规划的应用,涉及函数的奇偶性、单调性的综合应用,关键是利用函数的奇偶性与单调性分析得到关于x、b的不等式.

 小学课时特训系列答案
小学课时特训系列答案(1)写出每户每月用电量x度与支付费y元的函数关系;
(2)调查了该地120户家庭去年的月平均用电量,结果如下表:
| 月平均用电量x(度) | 90 | 140 | 200 | 260 | 320 |
| 频数 | 10 | 30 | 30 | 30 | 20 |
(3)今年用电形势严峻,该地政府决定适当下调a的值(170<a<180),小明家响应政府号召节约用电,预计他家今年的月平均电费为l15.2元,并且他家的月平均用电量X的分布列为:
| 月用电量X(度) | 160 | 300 | 180 |
| p | $\frac{1}{2}$ | $\frac{1}{6}$ | $\frac{1}{3}$ |
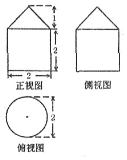
| A. | $\frac{7π}{3}$ | B. | $8+\frac{π}{3}$ | C. | $({4+\sqrt{2}})π$ | D. | $({5+\sqrt{2}})π$ |
 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=60°,AB=2AD,PD⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=60°,AB=2AD,PD⊥底面ABCD.