题目内容
(12分)过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线l作垂线,垂足分别为M1、N1.
(1)求证:FM1⊥FN1;
(2)记△FMM1、△FM1N1、△FNN1的面积分别为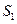 、
、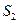 、
、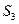 ,试判断S
,试判断S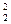 =4
=4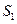
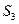 是否成立,并证明你的结论.
是否成立,并证明你的结论.
(1)求证:FM1⊥FN1;
(2)记△FMM1、△FM1N1、△FNN1的面积分别为
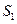 、
、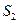 、
、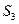 ,试判断S
,试判断S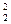 =4
=4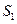
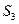 是否成立,并证明你的结论.
是否成立,并证明你的结论.(1)略
(2)略
(1)证法一:由抛物线的定义得|MF|=|MM1|,|NF|=|NN1|.
∴∠MFM1=∠MM1F,∠NFN1=∠NN1F.
如图,设准线l与x轴的交点为F1.
∵MM1∥NN1∥FF1,
∴∠F1FM1=∠MM1F,∠F1FN1=∠NN1F.
而∠F1FM1+∠MFM1+∠F1FN1+∠NFN1=180o,
即2∠F1FM1+2∠F1FN1=180o,
∴∠F1FM1+∠F1FN1=90o,
即∠M1FN1=90o,故FM1⊥FN1.
证法二:依题意,焦点为F( ,0),准线l的方程为x=-
,0),准线l的方程为x=- .
.
设点M,N的坐标分别为M(x1,y1),N(x2,y2),直线MN的方程为x=my+ ,则有M1(-
,则有M1(- ,y1),N1(-
,y1),N1(- ,y2),
,y2),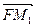 =(-p,y1),
=(-p,y1), 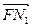 =(-p,y2).
=(-p,y2).
由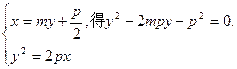
于是,y1+y2=2mp,y1y2=-p2.
∴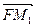 ·
·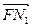 =p2+y1y2=p2-p2=0,故FM1⊥FN1.
=p2+y1y2=p2-p2=0,故FM1⊥FN1.
(2)S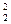 =4S1S3成立,证明如下:
=4S1S3成立,证明如下:
证法一:设M(x1,y1),N(x2,y2),
直线l与x轴的交点为F1,则由抛物线的定义得
|MM1|=|MF|=x1+ , |NN1|=|NF|=x2+
, |NN1|=|NF|=x2+ . 于是
. 于是
S1= ·|MM1|·|F1M1|=
·|MM1|·|F1M1|= (x1+
(x1+ )|y1|,
)|y1|,
S2= ·|M1N1|·|FF1|=
·|M1N1|·|FF1|= p|y1-y2|,
p|y1-y2|,
S3= ·|NN1|·|F1N1|=
·|NN1|·|F1N1|= (x2+
(x2+ )|y2|,
)|y2|,
∵S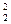 =4S1S3
=4S1S3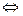 (
( p|y1-y2|)2
p|y1-y2|)2
=4× (x1+
(x1+ )|y1|·
)|y1|· (x2+
(x2+ )·|y2|
)·|y2|
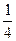 p2[(y1+y2)2-4y1y2]=[x1x2+
p2[(y1+y2)2-4y1y2]=[x1x2+ (x1+x2)+
(x1+x2)+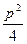 ]·|y1y2|.
]·|y1y2|.
将 与
与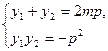 代入上式化简可得
代入上式化简可得
p2(m2p2+p2)=p2(m2p2+p2),此式恒成立. 故S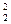 =4S1S3成立.
=4S1S3成立.
∴∠MFM1=∠MM1F,∠NFN1=∠NN1F.
如图,设准线l与x轴的交点为F1.
∵MM1∥NN1∥FF1,
∴∠F1FM1=∠MM1F,∠F1FN1=∠NN1F.
而∠F1FM1+∠MFM1+∠F1FN1+∠NFN1=180o,
即2∠F1FM1+2∠F1FN1=180o,
∴∠F1FM1+∠F1FN1=90o,
即∠M1FN1=90o,故FM1⊥FN1.
证法二:依题意,焦点为F(
 ,0),准线l的方程为x=-
,0),准线l的方程为x=- .
.设点M,N的坐标分别为M(x1,y1),N(x2,y2),直线MN的方程为x=my+
 ,则有M1(-
,则有M1(- ,y1),N1(-
,y1),N1(- ,y2),
,y2),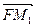 =(-p,y1),
=(-p,y1), 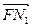 =(-p,y2).
=(-p,y2).由
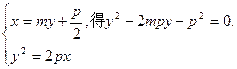
于是,y1+y2=2mp,y1y2=-p2.
∴
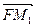 ·
·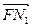 =p2+y1y2=p2-p2=0,故FM1⊥FN1.
=p2+y1y2=p2-p2=0,故FM1⊥FN1.(2)S
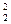 =4S1S3成立,证明如下:
=4S1S3成立,证明如下:证法一:设M(x1,y1),N(x2,y2),
直线l与x轴的交点为F1,则由抛物线的定义得
|MM1|=|MF|=x1+
 , |NN1|=|NF|=x2+
, |NN1|=|NF|=x2+ . 于是
. 于是S1=
 ·|MM1|·|F1M1|=
·|MM1|·|F1M1|= (x1+
(x1+ )|y1|,
)|y1|,S2=
 ·|M1N1|·|FF1|=
·|M1N1|·|FF1|= p|y1-y2|,
p|y1-y2|,S3=
 ·|NN1|·|F1N1|=
·|NN1|·|F1N1|= (x2+
(x2+ )|y2|,
)|y2|,∵S
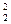 =4S1S3
=4S1S3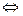 (
( p|y1-y2|)2
p|y1-y2|)2=4×
 (x1+
(x1+ )|y1|·
)|y1|· (x2+
(x2+ )·|y2|
)·|y2|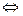
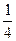 p2[(y1+y2)2-4y1y2]=[x1x2+
p2[(y1+y2)2-4y1y2]=[x1x2+ (x1+x2)+
(x1+x2)+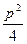 ]·|y1y2|.
]·|y1y2|.将
 与
与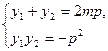 代入上式化简可得
代入上式化简可得p2(m2p2+p2)=p2(m2p2+p2),此式恒成立. 故S
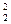 =4S1S3成立.
=4S1S3成立.
练习册系列答案
相关题目
 , 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。
, 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。 ,求点M的坐标
,求点M的坐标 ;
;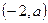 为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P。若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。
为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P。若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。 上任意两点(直线AB不垂直于
上任意两点(直线AB不垂直于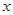 轴),线段AB的中垂线交
轴),线段AB的中垂线交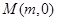 ,则
,则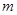 的取值范围是_______
的取值范围是_______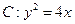 ,
,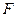 是抛物线
是抛物线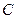 的焦点,过
的焦点,过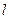 与
与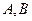 两点.
两点.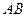 为直径的圆的方程;
为直径的圆的方程;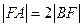 ,求直线
,求直线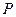 是抛物线
是抛物线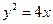 上一动点,则点
上一动点,则点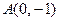 的距离与
的距离与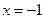 的距离和
的距离和 的最小值是( )
的最小值是( )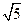

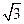
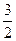
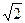
 是抛物线
是抛物线 上的一个动点,则点
上的一个动点,则点




 上,则这个正三角形的边长是 ( )
上,则这个正三角形的边长是 ( )



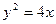 上的点
上的点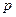 到抛物线的准线的距离为
到抛物线的准线的距离为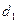 ,到直线
,到直线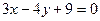 的距离为
的距离为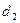 ,则
,则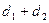 的最小值为 ( )
的最小值为 ( )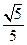
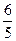
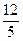
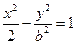 (a>0,b>0)的渐近线与抛物线
(a>0,b>0)的渐近线与抛物线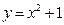 相切,则b等于( )
相切,则b等于( )


