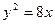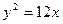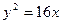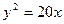题目内容
给定抛物线
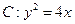 ,
,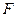 是抛物线
是抛物线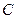 的焦点,过
的焦点,过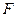 的直线
的直线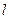 与
与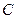 相交于
相交于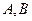 两点.
两点.(1)设直线
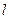 的斜率为1,求以
的斜率为1,求以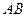 为直径的圆的方程;
为直径的圆的方程;(2)若
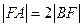 ,求直线
,求直线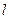 的方程.
的方程.(1)
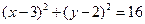
(2)
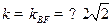
解:(1)设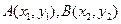 ,
,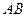 中点
中点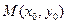 ,
,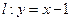 ,
,
联立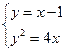 ,消去
,消去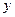 得
得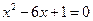 ,
,
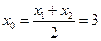 ,
,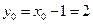 ,
,
故圆心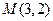 ,半径
,半径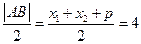 ,
,
从而以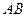 为直径的圆的方程为
为直径的圆的方程为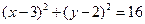 ;………………………………4分
;………………………………4分
(2)显然直线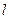 的斜率存在,故可设直线
的斜率存在,故可设直线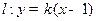 ,
,
联立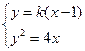 ,消去
,消去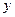 得
得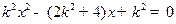 ,
,
则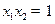 ,故
,故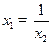
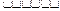 1,
1,
又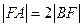 ,则
,则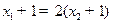
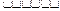 2,
2,
由12得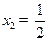 (
(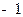 舍),所以
舍),所以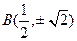 , 得直线
, 得直线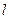 斜率为
斜率为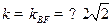
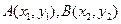 ,
,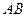 中点
中点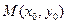 ,
,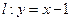 ,
,联立
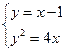 ,消去
,消去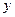 得
得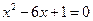 ,
,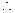
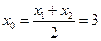 ,
,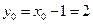 ,
,故圆心
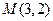 ,半径
,半径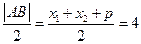 ,
,从而以
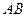 为直径的圆的方程为
为直径的圆的方程为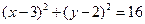 ;………………………………4分
;………………………………4分(2)显然直线
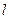 的斜率存在,故可设直线
的斜率存在,故可设直线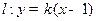 ,
,联立
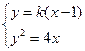 ,消去
,消去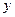 得
得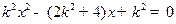 ,
,则
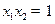 ,故
,故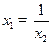
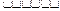 1,
1,又
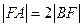 ,则
,则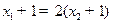
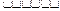 2,
2,由12得
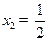 (
(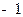 舍),所以
舍),所以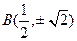 , 得直线
, 得直线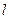 斜率为
斜率为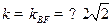

练习册系列答案
相关题目
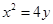 上一点P到定点A(0,1)的距离为2, 则P到x轴的距离为( )
上一点P到定点A(0,1)的距离为2, 则P到x轴的距离为( )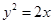 上的点P到直线y=2x+4有最短的距离,则P的坐标是( )
上的点P到直线y=2x+4有最短的距离,则P的坐标是( )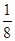 ,
,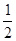 )
)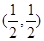
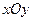 中,抛物线
中,抛物线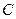 的顶点是坐标原点且经过点
的顶点是坐标原点且经过点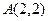 ,其焦点
,其焦点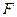 在
在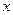 轴上,求抛物线方程.
轴上,求抛物线方程.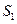 、
、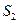 、
、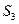 ,试判断S
,试判断S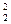 =4
=4 2x-y=4距离最近的点的坐标是( )
2x-y=4距离最近的点的坐标是( )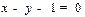 与抛物线
与抛物线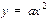 相切,则
相切,则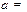
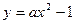 的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为
的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 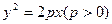 上有一点M,它的横坐标是3,它到焦点的距离是5,则抛物线的方程为(
上有一点M,它的横坐标是3,它到焦点的距离是5,则抛物线的方程为(  )
)