题目内容
4.实数x,y满足$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$,则z=4x+3y的最大值为( )| A. | 3 | B. | 4 | C. | 18 | D. | 24 |
分析 画出满足条件的平面区域,求出角点的坐标,结合函数的图象求出z的最大值即可.
解答 解:画出满足条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$的平面区域,如图示: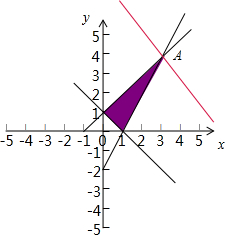 ,
,
由$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=2}\end{array}\right.$,解得A(3,4),
由z=4x+3y得:y=-$\frac{4}{3}$x+$\frac{1}{3}$z,
结合图象得直线过A(3,4)时,z最大,
z的最大值是24,
故选:D.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.设向量$\overrightarrow{a}$=(n,1),$\overrightarrow{b}$=(2,1),且|$\overrightarrow{a}$-$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2,则n=( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
12.设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面 的4个图形中,能表示集合M到集合N的函数关系的有( )
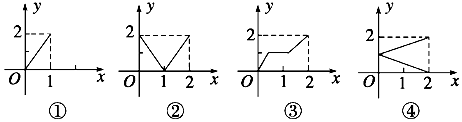
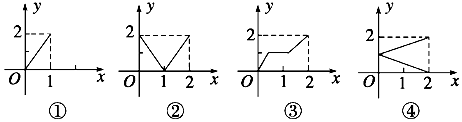
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
19.已知集合A={x|x2-3x+2<0},B={x|y=lg(3-x)},则A∩B=( )
| A. | {x|1<x<2} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|x<3} |
16.已知双曲线C$:\frac{x^2}{a^2}-\frac{y^2}{4}=1$的一条渐近线方程为2x+3y=0,F1,F2分别是双曲线C的左,右焦点,点P在双曲线C上,且|PF1|=7,则|PF2|等于( )
| A. | 1 | B. | 13 | C. | 4或10 | D. | 1或13 |
13.已知集合{x|x2+ax=0}={0,1},则实数a的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
11.若a,b∈R,且a>b,则下列不等式中恒成立的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | a2>b2 | C. | 2a>2b | D. | $\frac{a}{b}>1$ |