题目内容
设g（x）=cos（sinx）（0≤x≤π），求g（x）的最大值和最小值．
考点：三角函数的最值
专题：三角函数的求值
分析：由0≤x≤π，利用正弦函数的单调性可得0≤sinx≤1，再利用余弦函数的单调性即可得出g（x）的最值．
解答：
解：∵0≤x≤π，
∴0≤sinx≤1，
∴g（x）=cos（sinx）∈[cos1，1]．
∴g（x）的最大值和最小值分别为1，cos1．
∴0≤sinx≤1，
∴g（x）=cos（sinx）∈[cos1，1]．
∴g（x）的最大值和最小值分别为1，cos1．
点评：本题考查了正弦函数、余弦函数的单调性值域，考查了计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
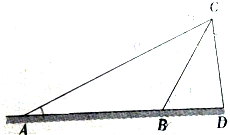为了测量一个塔的高度，某人站在A处测得塔尖C的仰角为30°，前进100m后达到B处，测得塔尖的仰角为75°，则该塔的高度为