题目内容

双曲线
y2
3
-x2=1的渐近线方程为（　　）
A、y=±
3
B、y=±
3
x
C、y=±
3
3
D、y=±
3
3
x
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：直接根据双曲线的方程，令方程的右边等于0求出渐近线的方程．
解答： 解：已知双曲线
y2
3
-x2=1，
令：
y2
3
-x2=0
即得到渐近线方程为：y=±
3
x
故选：B
点评：本题考查的知识要点：双曲线的渐渐线方程的求法．
练习册系列答案
相关题目
如图所示，△ABC的三边分别为a、b、c．
（1）若a、b、c满足a2=b2+c2-bc，求∠A的度数；
（2）在（1）的条件下，若b=3，c=4，求△ABC的面积．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点F，点E（
a2
c
，0）（c为椭圆的半焦距）在x轴上，若椭圆的离心率e=
2
2
，且|EF|=1．
（1）求椭圆方程；
（2）若过F的直线交椭圆与A，B两点，且
OA
+
OB
与向量
m
=（4，-
2
）共线（其中O为坐标原点），求证：
OA
•
OB
=0．
已知点A（2
6
，
3
5
）在椭圆
x2
a2
+
y2
9
=1上，则椭圆的离心率为（　　）
A、
4
5
B、
3
5
C、
5
3
D、
5
4
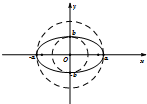圆锥曲线中不同曲线的性质都是有一定联系的，比如圆可以看成特殊的椭圆，所以很多圆的性质结论可以类比到椭圆，例如；如图所示，椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）可以被认为由圆x2+y2=a2作纵向压缩变换或由圆x2+y2=b2作横向拉伸变换得到的．依据上述论述我们可以推出椭圆C的面积公式为
 
．
已知双曲线的渐近线为y=±
3
x，焦点坐标为（-4，0），（4，0），则双曲线方程为（　　）
A、
x2
4
-
y2
12
=1
B、
x2
2
-
y2
4
=1
C、
x2
24
-
y2
8
=1
D、
x2
8
-
y2
24
=1
函数f（x）=
x2+4
1-x
+lg（3x+1）的定义域为（　　）
A、（-
1
3
，+∞）
B、（-∞，-
1
3
）
C、（-
1
3
，1）
D、（-
1
3
，
1
3
）
给出下列命题：
（1）函数f（x）=2xln（x-2）-3只有一个零点；
（2）若
a
与
b
不共线，则
a
+
b
与
a
-
b
不共线；
（3）若非零平面向量
a
，
b
，
c
两两所成的夹角均相等，则夹角为120°；
（4）若数列{an}的前n项的和Sn=2n+1-1，则数列{an}是等比数列；
（5）函数y=2x的图象经过一定的平移可以得到函数y=3•2x-1的图象．
其中，所有正确命题的序号为
 
．
在△ABC中，角A，B，C的对边分别为a，b，c，已知∠B=30°，△ABC的面积为
3
2
．
（Ⅰ）当a，b，c成等差数列时，求b；
（Ⅱ）求AC边上的中线BD的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网